
【题目】已知等差数列{an}的前n项和为Sn , a1=a,当n≥2时, ![]() =3n2an+S
=3n2an+S ![]() ,an≠0,n∈N*.
,an≠0,n∈N*.
(1)求a的值;
(2)设数列{cn}的前n项和为Tn , 且cn=3n﹣1+a5 , 求使不等式4Tn>S10成立的最小正整数n的值.
【答案】
(1)解:设等差数列{an}的公差为d.
当n≥2时, ![]() =3n2an+S
=3n2an+S ![]() ,an≠0,n∈N*.a1=a,
,an≠0,n∈N*.a1=a,
分别令n=2,3,可得: ![]() =12a2+a2,
=12a2+a2, ![]() =27a3+
=27a3+ ![]() .
.
∴(2a+d)2=12(a+d)+a2,2a+2a2+a3=27=5a+4d,
联立解得a=3,d=3
(2)解:由(1)可得:an=3+3(n﹣1)=3n.
Sn= ![]() =
= ![]() .
.
cn=3n﹣1+a5=15+3n﹣1.
∴数列{cn}的前n项和Tn= ![]() +15n=
+15n= ![]() +15n.
+15n.
不等式4Tn>S10,即:4×[ ![]() +15n]>
+15n]> ![]() .
.
化为:f(n)=23n+60n﹣167>0,
f(2)=﹣29<0,f(3)=67>0.
∴ ![]() 使不等式4Tn>S10成立的最小正整数n的值为3
使不等式4Tn>S10成立的最小正整数n的值为3
【解析】(1)设等差数列{an}的公差为d.当n≥2时, ![]() =3n2an+S
=3n2an+S ![]() ,an≠0,n∈N*.a1=a,分别令n=2,3,可得:
,an≠0,n∈N*.a1=a,分别令n=2,3,可得: ![]() =12a2+a2,
=12a2+a2, ![]() =27a3+
=27a3+ ![]() .化简解出即可得出.(2)由(1)可得:an=3n.Sn=
.化简解出即可得出.(2)由(1)可得:an=3n.Sn= ![]() .cn=3n﹣1+a5=15+3n﹣1.求得数列{cn}的前n项和Tn=
.cn=3n﹣1+a5=15+3n﹣1.求得数列{cn}的前n项和Tn= ![]() +15n.代入不等式4Tn>S10,化简即可得出.
+15n.代入不等式4Tn>S10,化简即可得出.
【考点精析】本题主要考查了等差数列的通项公式(及其变式)和数列的前n项和的相关知识点,需要掌握通项公式:![]() 或
或![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系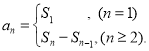 才能正确解答此题.
才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】己知函数f(x)= ![]() (其中e为自然对数的底数),h(x)=x﹣
(其中e为自然对数的底数),h(x)=x﹣ ![]() .
.
(I)求函数f(x)的单调区间;
(II)设g(x)= ![]() ,.已知直线y=
,.已知直线y= ![]() 是曲线y=f(x)的切线,且函数g(x)在(0,+∞)上是增函数.
是曲线y=f(x)的切线,且函数g(x)在(0,+∞)上是增函数.
(i)求实数a的值;
(ii)求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2x和圆x2+y2﹣x=0,倾斜角为 ![]() 的直线l经过抛物线的焦点,若直线l与抛物线和圆的交点自上而下依次为A,B,C,D,则|AB|+|CD|= .
的直线l经过抛物线的焦点,若直线l与抛物线和圆的交点自上而下依次为A,B,C,D,则|AB|+|CD|= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(1﹣m)lnx+ ![]() ﹣x,m∈R且m≠0.
﹣x,m∈R且m≠0.
(Ⅰ)当m=2时,令g(x)=f(x)+log2(3k﹣1),k为常数,求函数y=g(x)的零点的个数;
(Ⅱ)若不等式f(x)>1﹣ ![]() 在x∈[1,+∞)上恒成立,求实数m的取值范围.
在x∈[1,+∞)上恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义“正对数”:ln+x= ![]() ,现有四个命题: ①若a>0,b>0,则ln+(ab)=bln+a
,现有四个命题: ①若a>0,b>0,则ln+(ab)=bln+a
②若a>0,b>0,则ln+(ab)=ln+a+ln+b
③若a>0,b>0,则 ![]() b
b
④若a>0,b>0,则ln+(a+b)≤ln+a+ln+b+ln2
其中的真命题有: . (写出所有真命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《数学九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白,与著名的海伦公式完全等价,由此可以看出我国古代已具有很高的数学水平,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实.一为从隔,开平方得积.”若把以上这段文字写成公式,即S= ![]() .现有周长为4+
.现有周长为4+ ![]() 的△ABC满足sinA:sinB:sinC=(
的△ABC满足sinA:sinB:sinC=( ![]() ﹣1):
﹣1): ![]() : (
: ( ![]() +1),试用以上给出的公式求得△ABC的面积为( )
+1),试用以上给出的公式求得△ABC的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究家用轿车在高速公路上的车速情况,交通部门随机对50名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在30名男性驾驶员中,平均车速超过100km/h的有20人,不超过100km/h的有10人.在20名女性驾驶员中,平均车速超过100km/h的有5人,不超过100km/h的有15人.
(Ⅰ)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过100km/h的人与性别有关;
平均车速超过100km/h人数 | 平均车速不超过100km/h人数 | 合计 | |
男性驾驶员人数 | |||
女性驾驶员人数 | |||
合计 | |||
(Ⅱ)以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随机抽取3辆,记这3辆车中驾驶员为女性且车速不超过100km/h的车辆数为ζ,若每次抽取的结果是相互独立的,求ζ的分布列和数学期望.
参考公式: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
P(K2≥k0) | 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com