
(
温州十校模拟)如下图,四棱锥P—ABCD中,PA⊥ABCD,四边形ABCD是矩形.E、F分别是AB、PD的中点.若PA=AD=3,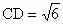 .
.
(1)
求证:AF∥平面PCE;(2)
求点F到平面PCE的距离;(3)
求直线FC与平面PCE所成角的大小.
|
解析: (1)取PC的中点G,连结EG,FG,
又由 F为PD的中点,则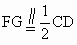 . .
又由已知有 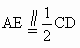 ,∴FG ,∴FG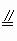 AE. AE.
∴四边形 AEGF是平行四边形.∴ AE∥EG.又 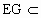 平面PCE. 平面PCE.
∴ AF∥平面PCE. (5分)(2) ∵PA⊥平面ABCD,∴平面 PAD⊥ABCD.由 ABCD是矩形有CD⊥AD.∴ CD⊥平面PAD.∴AF⊥CD.又 PA=AD=3,F是PD的中点,∴AF⊥PD.∵ PD∩CD=D,∵AF⊥平面PCD.由 EG∥AF,∴EG⊥平面PCD.∴在平面 PCD内,过F作FH⊥PC于H,由于平面 PCD∩平面PCE=PC,则FH的长就是点F到平面PCE的距离.(8 分)由已知可得
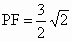 , ,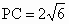 . .
由于 CD⊥平面PAD,∴∠CPD=30°.∴ ∴点 F到平面PCE的距离为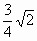 . (10分) . (10分)
(3) 由(2)知∠FCH为直线FC与平面PCE所成的角.在 Rt△CDF中,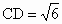 , ,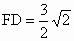 , ,
∴ ∴ ∴直线 FC与平面PCE所成角的大小为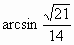 . (14分) . (14分) |


科目:高中数学 来源: 题型:013
(2007
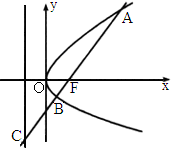
湖北十校模拟)如图所示,过抛物线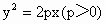 的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为
的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为
[
]
|
A .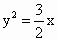 |
B .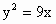 |
C .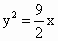 |
D .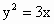 |
查看答案和解析>>
科目:高中数学 来源: 题型:044
(
温州十校模拟)已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点恰好是抛物线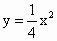 的焦点,离心率等于
的焦点,离心率等于 .
.
(1)
求椭圆C的标准方程;(2)
过椭圆C的右焦点作直线l交椭圆C于A、B两点,交y轴于M点,若 ,求证
,求证 为定值.
为定值.查看答案和解析>>
科目:高中数学 来源: 题型:013
(
温州十校模拟)已知两个不同的平面α、β和两条不重合的直线m、n,,有下列四个命题①若
m∥n,m⊥α,则n⊥α②若
m⊥α,m⊥β,则α∥β③若
m⊥α,m∥n,n β,则α⊥β
β,则α⊥β
④若
m∥α,α∩β=n,则m∥n其中正确命题的个数是
[
]|
? .?个 |
? .?个 |
|
C .2个 |
? D.?个 |
查看答案和解析>>
科目:高中数学 来源: 题型:044
(2007
湖北八校模拟)如下图,直三棱柱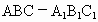 中,∠ACB=90°,
中,∠ACB=90°,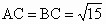 ,
,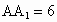 ,E、F分别为
,E、F分别为 与
与 的中点.
的中点.
(1)
求证:EF∥底面ABC;(2)
求平面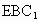 与平面ABC所成的锐二面角的大小.
与平面ABC所成的锐二面角的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com