
(
温州十校模拟)已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点恰好是抛物线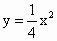 的焦点,离心率等于
的焦点,离心率等于 .
.
(1)
求椭圆C的标准方程;(2)
过椭圆C的右焦点作直线l交椭圆C于A、B两点,交y轴于M点,若 ,求证
,求证 为定值.
为定值. |
解析: (1)设椭圆C的方程为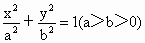 ,则由题意知b=1. ,则由题意知b=1.
∴ 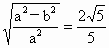 ,即 ,即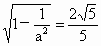 . .
∴ 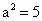 . .
∴椭圆 C的方程为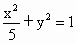 . (6分) . (6分)
(2) 解法一:设点A、B、M的坐标分别为 , , , ,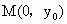 .易知F点的坐标为(2,0). .易知F点的坐标为(2,0).
∵ 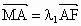 ,∴ ,∴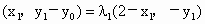 . .
∴ 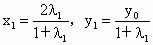 . (9分) . (9分)
将 A点的坐标代入到椭圆方程中,得 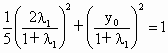 . .
去分母整理得 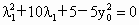 . (12分) . (12分)
同理,由 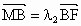 可得 可得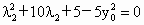 . .
∴ 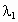 , ,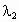 是方程 是方程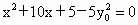 的两个根, 的两个根,
∴ 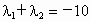 . (15分) . (15分)
解法二:设点 A、B、M的坐标分别为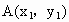 , , , ,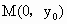 .又易知F点的坐标为(2,0). .又易知F点的坐标为(2,0).
显然直线 l存在斜率,设直线l的斜率为k,则直线l的方程是y=k(x-2).将直线l的方程代入到椭圆C的方程中,消去y并整理得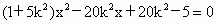 . (9分) . (9分)
∴ 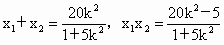 . (12分) . (12分)
又∵ 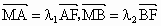 ,将各点坐标代入得 ,将各点坐标代入得
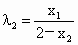 , ,
∴ 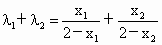  . (15分) . (15分) |


科目:高中数学 来源: 题型:044
(
温州十校模拟)已知函数 ,过点P(1,0)作曲线y=f(x)的两条切线PM、PN,切点分别为M、N.
,过点P(1,0)作曲线y=f(x)的两条切线PM、PN,切点分别为M、N.
(1)
当t=2时,求函数f(x)的单调递增区间;(2)
设|MN|=g(t),试求函数g(t)的表达式;(3)
在(2)的条件下,若对任意的正整数n,在区间 内总存在m+1个数
内总存在m+1个数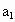 ,
, ,…,
,…, ,
, ,使得不等式
,使得不等式 成立,求m的最大值.
成立,求m的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:013
(
温州十校模拟)已知两个不同的平面α、β和两条不重合的直线m、n,,有下列四个命题①若
m∥n,m⊥α,则n⊥α②若
m⊥α,m⊥β,则α∥β③若
m⊥α,m∥n,n β,则α⊥β
β,则α⊥β
④若
m∥α,α∩β=n,则m∥n其中正确命题的个数是
[
]|
? .?个 |
? .?个 |
|
C .2个 |
? D.?个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com