
分析 (1)首先函数的定义域为(0,+∞),然后求出函数的导数f′(x),将f′(x)变形后,再结合x>0和b>$\frac{1}{2}$得f′(x)>0,可得函数f(x)在定义域(0,+∞)上单调递增;
(2)方程f′(x)=0在(0,+∞)有两个不相等的实数根时,函数有极值.然后利用根的判别式算得当b<$\frac{1}{2}$时,函数存在极值点,最后根据b≤0和0<b<$\frac{1}{2}$两种情况分别得出函数的极值点.
解答 解:(1)f′(x)=-2(x-1)-$\frac{b}{x}$=-$\frac{{2(x-\frac{1}{2})}^{2}+b-\frac{1}{2}}{x}$,
当b>$\frac{1}{2}$时,f′(x)<0,
函数f(x)在定义域(0,+∞)递减;
(2)①由(1),b>$\frac{1}{2}$时,函数f(x)无极值点,
②b=$\frac{1}{2}$时,有2个相同的解x=$\frac{1}{2}$,
∴b=$\frac{1}{2}$时,函数f(x)在(-1,+∞)无极值点,
③b<$\frac{1}{2}$时,f′(x)=0有两个不同的解,
x1=$\frac{1}{2}$-$\frac{\sqrt{1-2b}}{2}$,x2=$\frac{1}{2}$+$\frac{\sqrt{1-2b}}{2}$,
∴(i)b≤0时,x1=$\frac{1}{2}$-$\frac{\sqrt{1-2b}}{2}$≤0∉(0,+∞),舍去,
而x2=$\frac{1}{2}$+$\frac{\sqrt{1-2b}}{2}$≥1∈(0,+∞),
此时f′(x),f(x)随x在定义域上的变化情况如下表:
| x | (0,x2) | x2 | (x2,+∞) |
| f′(x) | + | 0 | - |
| f(x) | 递增 | 极大值 | 递减 |
| x | (0,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | 递减 | 极小值 | 递增 | 极大值 | 递减 |
点评 本题考查了利用导数研究函数的单调性和含有字母参数的函数极值的讨论,属于中档题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -4 | C. | -2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 单位向量都相等 | |
| B. | 长度相等且方向相反的两个向量不一定是共线向量 | |
| C. | 若$\overrightarrow a$,$\overrightarrow b$满足$|{\overrightarrow a}|$>$|{\overrightarrow b}|$且$\overrightarrow a$与$\overrightarrow b$同向,则$\overrightarrow a$>$\overrightarrow b$ | |
| D. | 对于任意向量$\overrightarrow a$,$\overrightarrow b$,必有$|{\overrightarrow a+\overrightarrow b}|$≤$|{\overrightarrow a}|$+$|{\overrightarrow b}|$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
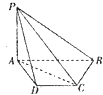 如图所示,四棱锥P-ABCD的底面为等腰梯形,AB∥DC,AB=2AD,若PA⊥平面ABCD,∠ABC=60°
如图所示,四棱锥P-ABCD的底面为等腰梯形,AB∥DC,AB=2AD,若PA⊥平面ABCD,∠ABC=60°查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{20}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2sin5 | B. | -2cos5 | C. | 2sin5 | D. | 2cos5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com