
分析 通过作差、利用|a|+|b|≥|a+b|,整理即得结论.
解答 证明:$\frac{|a|+|b|}{1+|a|+|b|}$-$\frac{|a+b|}{1+|a+b|}$
=$\frac{1}{(1+|a|+|b|)(1+|a+b|)}$[(|a|+|b|)(1+|a+b|)-(1+|a|+|b|)|a+b|]
=$\frac{1}{(1+|a|+|b|)(1+|a+b|)}$[|a|+|b|+|a+b|•|a|+|a+b|•|b|-(|a+b|+|a+b|•|a|+|a+b|•|b|)]
=$\frac{1}{(1+|a|+|b|)(1+|a+b|)}$(|a|+|b|-|a+b|)
≥0,
∴$\frac{|a|+|b|}{1+|a|+|b|}$≥$\frac{|a+b|}{1+|a+b|}$.
点评 本题考查不等式的证明,利用作差法是解决本题的关键,注意解题方法的积累,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
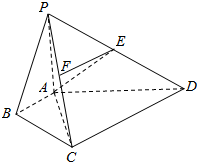 在四棱锥P-ABCD中,∠ABC=$\frac{π}{2}$,∠BAC=∠CAD=$\frac{π}{3}$,PA⊥平面ABCD,E为PD的中点,PA=2AB=2,CD=2$\sqrt{3}$.
在四棱锥P-ABCD中,∠ABC=$\frac{π}{2}$,∠BAC=∠CAD=$\frac{π}{3}$,PA⊥平面ABCD,E为PD的中点,PA=2AB=2,CD=2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{21}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {3} | C. | {1,3} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [1,2] | C. | [10,100] | D. | [0,lg2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 144 | B. | 480 | C. | 216 | D. | 432 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com