
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{7}{4}$ |
分析 求得圆的标准方程,求得圆心,由圆的对称性,求得ax-by=0过($\frac{3}{2}$,2),求得$\frac{b}{a}$=$\frac{3}{4}$,根据双曲线的离心率公式即可求得双曲线的离心率公式.
解答 解:圆x2+y2-3x-4y-5=0的标准方程:(x-$\frac{3}{2}$)2+(y-2)2=$\frac{45}{4}$,则圆心($\frac{3}{2}$,2),
由圆的对称性可知ax-by=0过($\frac{3}{2}$,2),整理得:$\frac{b}{a}$=$\frac{3}{4}$,
则双曲线的离心率e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\frac{5}{4}$,
则双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率$\frac{5}{4}$,
故答案为:$\frac{5}{4}$.
点评 本题考查双曲线的离心率公式,圆的标准方程,考查计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
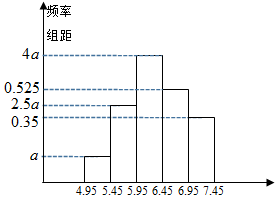 质检部门抽查某批次产品的质量(单位:克),随机检查了其中80件产品,根据样本数据描绘的频率分布直方图如下:
质检部门抽查某批次产品的质量(单位:克),随机检查了其中80件产品,根据样本数据描绘的频率分布直方图如下:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\sqrt{3}$-1] | B. | (-∞,0] | C. | [0,$\sqrt{3}$-1] | D. | (-∞,1-$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,2018) | B. | (4,2020) | C. | (3,2020) | D. | (2,2020) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3] | B. | [3,+∞) | C. | $(1,\frac{{3\sqrt{2}}}{4}]$ | D. | $[\frac{{3\sqrt{2}}}{4},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com