
分析 根据题意,分2步进行分析:①、先将5名学生分成3组,②、将分好的3组全排列,对应3 个社团,分别求出每一步的情况数目,由分步计数原理计算可得答案.
解答 解:根据题意,分2步进行分析:
①、先将5名学生分成3组,
若分成2、2、1的三组,有$\frac{{C}_{5}^{2}{C}_{3}^{2}{C}_{1}^{1}}{{A}_{2}^{2}}$=15种分组方法,
若分成3、1、1的三组,有$\frac{{C}_{5}^{3}{C}_{2}^{1}{C}_{1}^{1}}{{A}_{2}^{2}}$=10种分组方法,
则共有15+10=25种分组方法,
②、将分好的3组全排列,对应3 个社团,有A33=6种情况,
则不同的选择方案有25×6=150种;
故答案为:150.
点评 本题考查排列、组合的综合应用,注意要先分组,再进行排列.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:选择题
已知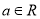 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分也非必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
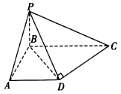 如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥PD,异面直线PA与CD所成角等于60°.
如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥PD,异面直线PA与CD所成角等于60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{7}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com