
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 62 | 68 | 75 | 81 | 89 |
分析 根据回归直线方程$\widehat{y}$=0.67x+a的图象过样本中心点($\overline{x}$,$\overline{y}$),求出平均数代入方程即可求出a的值.
解答 解:由题意,计算$\overline{x}$=$\frac{1}{5}$×(10+20+30+40+50)=30,
$\overline{y}$=$\frac{1}{5}$×(62+68+75+81+89)=75,
且回归直线方程 $\widehat{y}$=0.67x+a的图象过样本中心点($\overline{x}$,$\overline{y}$),
所以a=75-0.67×30=54.9.
故答案为:54.9.
点评 本题考查了回归直线方程的图象过样本中心点的应用问题,是基础题目.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:选择题
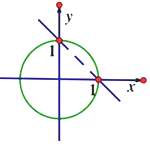
| A. | (x+y-1)•(x2+y2-1)=0 | B. | $\sqrt{x+y-1}•({x^2}+{y^2}-1)=0$ | ||
| C. | $(x+y-1)•\sqrt{{x^2}+{y^2}-1}=0$ | D. | $\sqrt{x+y-1}•\sqrt{{x^2}+{y^2}-1}=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{7}{3}$ | C. | $\frac{3}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 与教育有关 | 与教育无关 | 合计 | |
| 男 | 30 | 10 | 40 |
| 女 | 35 | 5 | 40 |
| 合计 | 65 | 15 | 80 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.023 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com