Question

8．若P为△ABC所在平面内的一点，满足 $\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{AB}$，则点P的位置为（　　）

• A． P在△ABC的内部
• B． P在△ABC的外部
• C． P在AB边所在的直线上
• D． P在AC边所在的直线上

Answer 1

分析 用向量的运算法则将等式变形，得到$\overrightarrow{PC}$=-2 $\overrightarrow{PA}$，据三点共线的充要条件得出结论：P在AC边所在的直线上．

解答 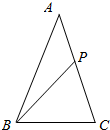解：∵$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{AB}$，
∴$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{PB}$-$\overrightarrow{PA}$，
∴$\overrightarrow{PC}$=-2 $\overrightarrow{PA}$=2$\overrightarrow{AP}$，
∴P是AC边的一个三等分点．
故选：D．

点评 本题考查了向量的加法及其几何意义．分析出$\overrightarrow{PC}$=-2 $\overrightarrow{PA}$是解题的难点．