Question

【题目】某地级市共有200000中小学生，其中有7%学生在2017年享受了“国家精准扶贫”政策，在享受“国家精准扶贫”政策的学生中困难程度分为三个等次：一般困难、很困难、特别困难，且人数之比为5:3:2，为进一步帮助这些学生，当地市政府设立“专项教育基金”，对这三个等次的困难学生每年每人分别补助1000元、1500元、2000元。经济学家调查发现，当地人均可支配年收入较上一年每增加，一般困难的学生中有会脱贫，脱贫后将不再享受“精准扶贫”政策，很困难的学生中有转为一般困难，特别困难的学生中有转为很困难。现统计了该地级市2013年到2017年共5年的人均可支配年收入，对数据初步处理后得到了如图所示的散点图和表中统计量的值，其中年份取13时代表2013年， 与（万元）近似满足关系式，其中为常数。（2013年至2019年该市中学生人数大致保持不变）

其中，

（Ⅰ）估计该市2018年人均可支配年收入；

（Ⅱ）求该市2018年的“专项教育基金”的财政预算大约为多少？

附：对于一组具有线性相关关系的数据，其回归直线方程 的斜率和截距的最小二乘估计分别为

Answer 1

【答案】（Ⅰ）2.8（万）;（Ⅱ）1624万.

【解析】

根据表中数据求出回归方程的系数，从而得到回归直线方程，代入，即可解出结果

由题意知年时该市享受“国家精准扶贫”政策的学生共人，一般困难、很困难、特别困难的中学生依次为人，人，人，按照增长比例关系求解年时该市享受“国家精准扶贫”政策的学生，即可求出财政预算。

（Ⅰ）因为，所以.

由得，

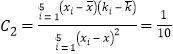所以 ， ，所以，所以.

当时，2018年人均可支配年收入（万）

（Ⅱ）由题意知2017年时该市享受“国家精准扶贫”政策的学生共200000×7%=14000人

一般困难、很困难、特别困难的中学生依次有7000人、4200人、2800人， 2018年人均可支配收入比2017年增长

所以2018年该市特别困难的中学生有2800×(1-10%)=2520人，

很困难的学生有4200×(1-20%)+2800×10%=3640人

一般困难的学生有7000×(1-30%)+4200×20%=5740人.

所以2018年的“专项教育基金”的财政预算大约为5740×1000+3640×1500+2520×2000=1624万.