练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若集合A={y|y=x
    1
    3
    ，-1≤x≤1}，B={y|y=(
    1
    2
    )x    ，x≤0}，则A∩B等于（　　）
    A、（-∞，-1）B、[-1，1]
    C、∅D、{1}
    分析：先利用求函数的值域的方法化简集合A，B，后求它们的交集．
    解答：解：∵A={y|y=x
    1
    3
    ，-1≤x≤1}={y|-1≤y≤1}，
    ∵B={y|y=(
    1
    2
    )x    ，x≤0}={y|y≥1}，
    ∴A∩B={1}．
    故选D．
    点评：集合中的运算包括集合之间的子集、交集、并集和补集运算．这类集合问题都是以基本题的身份出现在高考试卷中，解答时应正确地掌握集合的概念，理解集合的含义，将集合等价变形，利用数轴或韦恩图进一步研究集合的运算．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若集合A={y|y=x3，0≤x≤1}，集合B={y|y=
    1
    x
    ，0＜x≤1}    ，则A∩CRB等于（　　）
    A、[0，1]B、[0，1）
    C、（1，+∞）D、{1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若集合A={y|y=cosx，x∈R}，B={x|y=lnx}，则A∩B=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若集合A={y|y=log2x，0＜x≤1}，B={y|y=(
    12
    )x，x≤0}    ，则A∩B=
    ∅
    ∅
    ．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江苏省盐城市高三上学期期中考数学试卷（解析版） 题型：解答题

    已知函数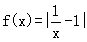

    （Ⅰ）判断f(x)在上的单调性，并证明你的结论；

    （Ⅱ）若集合A={y | y=f(x)，}，B=[0,1]， 试判断A与B的关系；

    （Ⅲ）若存在实数a、b(a<b)，使得集合{y | y=f(x)，a≤x≤b}=[ma，mb]，求非零实数m的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年浙江省杭州二中高一（上）期中数学试卷（解析版） 题型：选择题

    若集合A={y|y=}，B={y|y=3-x}，则A∪B=（ ）
    A．{y|y＞0}
    B．{y|y≥0}
    C．{y|y＞1}
    D．{y|y≥1}

    查看答案和解析>>

    同步练习册答案