
【题目】设椭圆 ![]() 1(a>
1(a> ![]() )的右焦点为F,右顶点为A,已知
)的右焦点为F,右顶点为A,已知 ![]() ,其中O为原点,e为椭圆的离心率.
,其中O为原点,e为椭圆的离心率.
(1)求椭圆的方程;
(2)设过点A的直线l与椭圆交于B(B不在x轴上),垂直于l的直线与l交于点M,与y轴交于点H,若BF⊥HF,且∠MOA=∠MAO,求直线l的斜率.
【答案】
(1)
解:由 ![]() ,
,
得 ![]() +
+ ![]() =
= 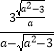 ,
,
即 ![]() =
= ![]() ,
,
∴a[a2﹣(a2﹣3)]=3a(a2﹣3),解得a=2.
∴椭圆方程为 ![]() ;
;
(2)
解:由已知设直线l的方程为y=k(x﹣2),(k≠0),
设B(x1,y1),M(x0,k(x0﹣2)),
∵∠MOA=∠MAO,
∴x0=1,
再设H(0,yH),
联立 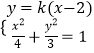 ,得(3+4k2)x2﹣16k2x+16k2﹣12=0.
,得(3+4k2)x2﹣16k2x+16k2﹣12=0.
△=(﹣16k2)2﹣4(3+4k2)(16k2﹣12)=144>0.
由根与系数的关系得 ![]() ,
,
∴ ![]() ,
, ![]() ,
,
MH所在直线方程为y﹣k(x0﹣2)=﹣ ![]() (x﹣x0),
(x﹣x0),
令x=0,得yH=(k+ ![]() )x0﹣2k,
)x0﹣2k,
∵BF⊥HF,
∴ ![]() ,
,
即1﹣x1+y1yH=1﹣ ![]() [(k+
[(k+ ![]() )x0﹣2k]=0,
)x0﹣2k]=0,
整理得: ![]() =1,即8k2=3.
=1,即8k2=3.
∴k=﹣ ![]() 或k=
或k= ![]()
【解析】(1)由题意画出图形,把|OF|、|OA|、|FA|代入 ![]() +
+ ![]() =
= ![]() ,转化为关于a的方程,解方程求得a值,则椭圆方程可求;
,转化为关于a的方程,解方程求得a值,则椭圆方程可求;
(2)由已知设直线l的方程为y=k(x﹣2),(k≠0),联立直线方程和椭圆方程,化为关于x的一元二次方程,利用根与系数的关系求得B的坐标,再写出MH所在直线方程,求出H的坐标,由BF⊥HF,得 ![]() ,整理得到M的坐标与k的关系,由∠MOA=∠MAO,得到x0=1,转化为关于k的等式求得k的值.
,整理得到M的坐标与k的关系,由∠MOA=∠MAO,得到x0=1,转化为关于k的等式求得k的值.
本题考查椭圆方程的求法,考查直线与椭圆位置关系的应用,体现了“整体运算”思想方法和“设而不求”的解题思想方法,考查运算能力,是难题.


科目:高中数学 来源: 题型:
【题目】如图,曲线![]() 由曲线
由曲线![]() 和曲线
和曲线![]() 组成,其中点
组成,其中点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点,点
所在圆锥曲线的焦点,点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点,
所在圆锥曲线的焦点,

(1)若![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(2)如图,作直线![]() 平行于曲线
平行于曲线![]() 的渐近线,交曲线
的渐近线,交曲线![]() 于点
于点![]() ,
,
求证:弦![]() 的中点
的中点![]() 必在曲线
必在曲线![]() 的另一条渐近线上;
的另一条渐近线上;
(3)对于(1)中的曲线![]() ,若直线
,若直线![]() 过点
过点![]() 交曲线
交曲线![]() 于点
于点![]() ,求△
,求△![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)数列{bn}的前n项和为Sn,求证:数列{Sn+![]() }是等比数列.
}是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l:x-y-2=0,抛物线C:y2=2px(p>0).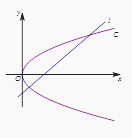
(1)若直线l过抛物线C的焦点,求抛物线C的方程;
(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.
①求证:线段PQ的中点坐标为(2-p , -p);
②求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)△ABC中,角A,B,C所对的边分别为a,b,c.已知a=3,cos A=![]() ,B=A+
,B=A+![]() .
.
(1)求b的值;
(2)求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:x2+y2﹣2ay=0(a>0)截直线x+y=0所得线段的长度是2 ![]() ,则圆M与圆N:(x﹣1)2+(y﹣1)2=1的位置关系是( )
,则圆M与圆N:(x﹣1)2+(y﹣1)2=1的位置关系是( )
A.内切
B.相交
C.外切
D.相离
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=xlnx﹣ax2+(2a﹣1)x,a∈R.
(1)令g(x)=f′(x),求g(x)的单调区间;
(2)已知f(x)在x=1处取得极大值,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2e2x+m|x|ex+1(m∈R)有四个零点,则m的取值范围为( )
A.(﹣∞,﹣e﹣ ![]() )
)
B.(﹣∞,e+ ![]() )
)
C.(﹣e﹣ ![]() ,﹣2)
,﹣2)
D.(﹣∞,﹣ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com