
【题目】(本小题满分12分)△ABC中,角A,B,C所对的边分别为a,b,c.已知a=3,cos A=![]() ,B=A+
,B=A+![]() .
.
(1)求b的值;
(2)求△ABC的面积.
【答案】(1) ![]() . (2)
. (2) ![]()
【解析】
试题分析:(1) 已知两角及对边求另一对边,应该利用正弦定理,在△ABC中,sin A=![]() ,sin B=sin
,sin B=sin![]() =cos A=
=cos A=![]() ,由正弦定理可得,b=
,由正弦定理可得,b=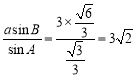
(2)三角形面积公式选用S=![]() absin C,则需求出sin C,sin C=sin[π-(A+B)] =sin(A+B) =sin Acos B+cos Asin B=
absin C,则需求出sin C,sin C=sin[π-(A+B)] =sin(A+B) =sin Acos B+cos Asin B=![]() ×
×![]() +
+![]() ×
×![]() =
=![]() .因此△ABC的面积S=
.因此△ABC的面积S=![]() absin C=
absin C=![]() ×3×
×3×![]() ×
×![]() =
=![]() .
.
试题解析:(1)在△ABC中,
由题意知,sin A=![]()
又因为B=A+![]() ,
,
所以sin B=sin![]() =cos A=
=cos A=![]()
由正弦定理可得,b=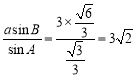 6分
6分
(2)由B=A+![]() 得cos B=cos
得cos B=cos![]() =-sin A=-
=-sin A=-![]() .
.
由A+B+C=π,得C=π-(A+B),
所以sin C=sin[π-(A+B)]
=sin(A+B)
=sin Acos B+cos Asin B
=![]() ×
×![]() +
+![]() ×
×![]()
=![]() .
.
因此△ABC的面积S=![]() absin C=
absin C=![]() ×3×
×3×![]() ×
×![]() =
=![]() . 12分
. 12分


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
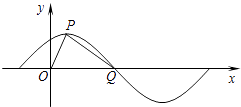
【题目】已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ< ![]() )图象如图,P是图象的最高点,Q为图象与x轴的交点,O为原点.且|OQ|=2,|OP|=
)图象如图,P是图象的最高点,Q为图象与x轴的交点,O为原点.且|OQ|=2,|OP|= ![]() ,|PQ|=
,|PQ|= ![]() .
. 
(1)求函数y=f(x)的解析式;
(2)将函数y=f(x)图象向右平移1个单位后得到函数y=g(x)的图象,当x∈[0,2]时,求函数h(x)=f(x)g(x)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得 =80, =20, i=184, =720.
(1)求家庭的月储蓄y对月收入x的线性回归方程![]() ;
;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程![]() 中,
中, ![]() ,其中
,其中![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,ABCD﹣A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1 , B1C1的中点,P是上底面的棱AD上的一点,AP= ![]() ,过P、M、N的平面交上底面于PQ,Q在CD上,则PQ= .
,过P、M、N的平面交上底面于PQ,Q在CD上,则PQ= . 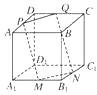
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,AB=5,AC=4,BC=3,AA1=4,D是AB的中点.
(Ⅰ)求证:AC⊥B1C;
(Ⅱ)求证:AC1∥平面B1CD
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆心为
,圆心为![]() ,定点
,定点![]() ,
, ![]() 为圆
为圆![]() 上一点,线段
上一点,线段![]() 上一点
上一点![]() 满足
满足![]() ,直线
,直线![]() 上一点
上一点![]() ,满足
,满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)![]() 为坐标原点,
为坐标原点, ![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与
与![]() 相切,并与轨迹
相切,并与轨迹![]() 交于不同的两点
交于不同的两点![]() .当
.当![]() 且满足
且满足![]() 时,求
时,求![]() 面积
面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com