
【题目】设a>0,b>0( )
A.若lna+2a=lnb+3b,则a>b
B.2a+2a=2b+3b,则a<b
C.若lna﹣2a=lnb﹣3b,则a>b
D.2a﹣2a=2b﹣3b,则a<b
【答案】A
【解析】解:∵lna+2a=lnb+3b,
∴a>0,b>0,
∴lna+2a=lnb+2b+b,
∴lna+2a>lnb+2b,
∵y=lnx+2x是增函数,
∴a>b.所以A正确;
同理B错误;
lna﹣2a=lnb﹣3b,
∴a>0,b>0,
∴lna﹣2a=lnb﹣2b﹣b,
∴lna﹣2a<lnb﹣2b,构造函数f(x)=lnx﹣2x,
则f′(x)= ![]() ﹣2<0,
﹣2<0,
故f(x)在(1,+∞)单调递减,
∴a>b,0<x<1时,
y=lnx﹣2x是增函数,
∴a<b.所以C不正确;
同理D不正确.
故选:A.
【考点精析】本题主要考查了命题的真假判断与应用和对数的运算性质的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系;①加法:![]() ②减法:
②减法:![]() ③数乘:
③数乘:![]() ④
④![]() ⑤
⑤![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图ABCD是平面四边形,∠ADB=∠BCD=90°,AB=4,BD=2.
(Ⅰ)若BC=1,求AC的长;
(Ⅱ)若∠ACD=30°,求tan∠BDC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,AB、BC、BD两两垂直,AB=BC=BD=4,E、F分别为棱BC、AD的中点. 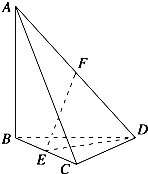
(1)求异面直线AB与EF所成角的余弦值;
(2)求E到平面ACD的距离;
(3)求EF与平面ACD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知(1+3x)n的展开式中,末三项的二项式系数的和等于121,求:
(1) 展开式中二项式系数最大的项;
(2) 展开式中系数最大的项.(结果可以以组合数形式表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某竞赛的题库系统有60%的自然科学类题目,40%的文化生活类题目(假设题库中的题目总数非常大),参赛者需从题库中抽取3个题目作答,有两种抽取方法:方法一是直接从题库中随机抽取3个题目;方法二是先在题库中按照题目类型用分层抽样的方法抽取10个题目作为样本,再从这10个题目中任意抽取3个题目.
(1)两种方法抽取的3个题目中,恰好有1个自然科学类题目和2个文化生活类题目的概率是否相同?若相同,说明理由;若不同,分别计算出两种抽取方法对应的概率.
(2)已知某参赛者抽取的3个题目恰好有1个自然科学类题目和2个文化生活类题目,且该参赛者答对自然科学类题目的概率为![]() ,答对文化生活类题目的概率为
,答对文化生活类题目的概率为![]() .设该参赛者答对的题目数为X,求X的分布列和数学期望.
.设该参赛者答对的题目数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,a2=3,a5=81,bn=1+2log3an .
(1)求数列{bn}的前n项的和;
(2)已知数列 ![]() 的前项的和为Sn , 证明:
的前项的和为Sn , 证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过对K2的统计量的研究,得到了若干个观测值,当K2≈6.706时,我们认为两分类变量A、B( )
A. 有67.06%的把握认为A与B有关系 B. 有99%的把握认为A与B有关系
C. 有0.010的把握认为A与B有关系 D. 没有充分理由说明A与B有关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为提升学生的英语学习能力,进行了主题分别为“听”、“说”、“读”、“写”四场竞赛.规定:每场竞赛的前三名得分分别为![]() ,
,![]() ,
,![]() (
(![]() ,且
,且![]() ,
,![]() ,
,![]() ),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终分为
),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终分为![]() 分,乙最终得分为
分,乙最终得分为![]() 分,丙最终得分为
分,丙最终得分为![]() 分,且乙在“听”这场竞赛中获得了第一名,则“听”这场竞赛的第三名是( )
分,且乙在“听”这场竞赛中获得了第一名,则“听”这场竞赛的第三名是( )
A. 甲 B. 乙 C. 丙 D. 甲和丙都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos ![]() ,g(x)=exf(x),其中e为自然对数的底数.
,g(x)=exf(x),其中e为自然对数的底数.
(1)求曲线y=g(x)在点(0,g(0))处的切线方程;
(2)若对任意 ![]() 时,方程g(x)=xf(x)的解的个数,并说明理由.
时,方程g(x)=xf(x)的解的个数,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com