
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() 与
与![]() 交于点
交于点![]() .
.
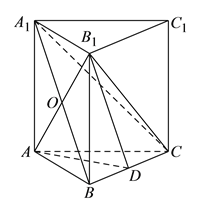
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的表面积.
的表面积.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)证明:连结![]() ,可得
,可得![]() 为
为![]() 的中位线,可得
的中位线,可得![]() ,根据线面平行的判定定理可得
,根据线面平行的判定定理可得![]() 平面
平面![]() ;(2)在直三棱柱
;(2)在直三棱柱![]() 中,可证
中,可证![]() 平面
平面![]() ,从而可得
,从而可得![]() ,又
,又![]() ,
,![]() ,即可证明
,即可证明![]() 平面
平面![]() ;(3)
;(3)![]() ,分别利用三角形面积公式求出各三角形面积,求和即可得结果.
,分别利用三角形面积公式求出各三角形面积,求和即可得结果.
试题解析:(1)证明:连结![]() ,
,
∵直三棱柱![]() ,
,![]() ,
,
∴四边形![]() 为正方形,
为正方形,
∴![]() 为
为![]() 中点,
中点,
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)证明:方法1,∵直三棱柱![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵正方形![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 平面
平面![]() .
.
方法2:∵直三棱柱![]() ,
,
∴平面![]() 平面
平面![]() ,
,
∵平面![]() 平面
平面![]() ,
,![]() ,
,
∵![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵正方形![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 平面
平面![]() .
.
(3)![]()
![]()
![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、线面垂直的判定定理、利用等积变换求三棱锥体积,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


科目:高中数学 来源: 题型:
【题目】已知关于x的不等式ax2+5x+c>0的解集为{x| ![]() <x<
<x< ![]() },
},
(1)求a,c的值;
(2)解关于x的不等式ax2+(ac+b)x+bc≥0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,动圆![]() 与圆
与圆![]() 外切,且与直线
外切,且与直线![]() 相切,记圆心
相切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设过定点![]() (
(![]() 为非零常数)的动直线
为非零常数)的动直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,问:在曲线
两点,问:在曲线![]() 上是否存在点
上是否存在点![]() (与
(与![]() 两点相异),当直线
两点相异),当直线![]() 的斜率存在时,直线
的斜率存在时,直线![]() 的斜率之和为定值.若存在,求出点
的斜率之和为定值.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列说法:
①y=sinx+cosx在区间(﹣ ![]() ,
, ![]() )内单调递增;
)内单调递增;
②存在实数α,使sinαcosα= ![]() ;
;
③y=sin( ![]() +2x)是奇函数;
+2x)是奇函数;
④x= ![]() 是函数y=cos(2x+
是函数y=cos(2x+ ![]() )的一条对称轴方程.
)的一条对称轴方程.
其中正确说法的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin ![]() cos
cos ![]() ﹣2
﹣2 ![]() sin2
sin2 ![]() +
+ ![]()
(1)求函数f(x)的单调减区间
(2)已知α∈( ![]() ,
, ![]() ),且f(α)=
),且f(α)= ![]() ,求f(
,求f( ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,且
是菱形,且![]() ,点
,点![]() 是棱
是棱![]() 的中点,平面
的中点,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
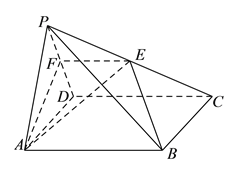
(![]() )求证:
)求证: ![]() .
.
(![]() )若
)若![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
求①二面角![]() 的锐二面角的余弦值.
的锐二面角的余弦值.
②在线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角等于
所成角等于![]() ,若存在,确定
,若存在,确定![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 的
的
部分图像如图所示.
(Ⅰ)求函数![]() 的解析式及
的解析式及![]() 图像的对称轴方程;
图像的对称轴方程;
(Ⅱ)把函数![]() 图像上点的横坐标扩大到原来的
图像上点的横坐标扩大到原来的![]() 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移
![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求关于
的图象,求关于![]() 的方程
的方程![]()
在![]() 时所有的实数根之和.
时所有的实数根之和.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com