【题目】已知关于x的不等式ax2+5x+c＞0的解集为{x| 
＜x＜ 
}，
（1）求a，c的值；
（2）解关于x的不等式ax2+（ac+b）x+bc≥0．
【答案】
（1）解：由题得a＜0且 
， 
是方程ax2+5x+c=0的两个实数根
则 
=﹣ 
， 
= 
，解得a=﹣6，c=﹣1，
（2）解：由a=﹣6，c=﹣1，原不等式化为﹣x2+（6+b）x﹣b≥0，
即（6x﹣b）（x﹣1）≤0．
①当 
即b＞6时，原不等式的解集为[1， 
]；
②当 =1即b=6时，原不等式的解集为{1}；
③当 
1即b＜6时，原不等式的解集为[ ，1]；
综上所述：当即b＞6时，原不等式的解集为[1， ]；
当b=6时，原不等式的解集为{1}；
当b＜6时，原不等式的解集为[ ，1]；
【解析】（1）根据韦达定理即可求出a，c的值，（2）需要分类讨论，然后求出解集即可．
【考点精析】关于本题考查的解一元二次不等式，需要了解求一元二次不等式
解集的步骤：一化：化二次项前的系数为正数;二判：判断对应方程的根;三求：求对应方程的根;四画：画出对应函数的图象;五解集：根据图象写出不等式的解集;规律：当二次项系数为正时，小于取中间，大于取两边才能得出正确答案．
科目：高中数学 来源： 题型：
【题目】设数列
的前n项和为
，
，且对任意正整数n，点(
，)在直线
上．
(1)求数列的通项公式；
(2)是否存在实数λ，使得数列{
}为等差数列？若存在，求出λ的值；若不存在，请说明理由；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在梯形
中， 
， 
. 
，且
平面
， 
，点
为
上任意一点.
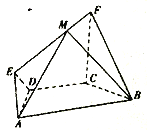
（1）求证： 
；
（2）点
在线段
上运动（包括两端点），若平面
与平面
所成的锐二面角为60°，试确定点
的位置．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N （异于村庄A),要求PM＝PN＝MN＝2（单位:千米)．如何设计, 可以使得工厂产生的噪声对居民的影响最小（即工厂与村庄的距离最远)．
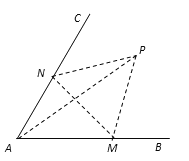
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
关于直线
对称，圆心
在第二象限，半径为
．
（Ⅰ）求圆的方程．
（Ⅱ）是否存在直线
与圆相切，且在
轴、
轴上的截距相等？若存在，写出满足条件的直线条数（不要求过程）；若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A.在（0， 
）内，sinx＞cosx
B.函数y=2sin（x+ 
）的图象的一条对称轴是x= 
π
C.函数y= 
的最大值为π
D.函数y=sin2x的图象可以由函数y=sin（2x﹣ 
）的图象向右平移 
个单位得到
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
