
分析 根据点与直线的关系,构造等差数列,利用等差数列的通项公式进行求解即可.
解答 解:∵点($\frac{{a}_{n}}{n}$,$\frac{{a}_{n+1}}{n+1}$)在直线x-y+1=0上,
∴$\frac{{a}_{n}}{n}$-$\frac{{a}_{n+1}}{n+1}$+1=0,
即$\frac{{a}_{n+1}}{n+1}$-$\frac{{a}_{n}}{n}$=1,
故数列{$\frac{{a}_{n}}{n}$}是公差为1的等差数列,首项为$\frac{{a}_{1}}{1}$=1,
则$\frac{{a}_{n}}{n}$=1+n-1=n,
则an=n2,
故答案为:n2
点评 本题主要考查数列通项公式的求解,根据点与直线关系,利用构造法是解决本题的关键.


科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥底面ABCD,BC=4,AB=PA=2,M为线段PC的中点,N在线段BC上,且BN=1.
如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥底面ABCD,BC=4,AB=PA=2,M为线段PC的中点,N在线段BC上,且BN=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
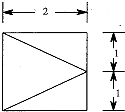 已知四棱锥,它的底面是边长为2的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数有3个,该四棱锥的体积为$\frac{4}{3}$.
已知四棱锥,它的底面是边长为2的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数有3个,该四棱锥的体积为$\frac{4}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )| A. | AC⊥SB | |
| B. | AB∥平面SCD | |
| C. | AC⊥面SBD | |
| D. | AB与SC所成的角等于DC与SA所成的角 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
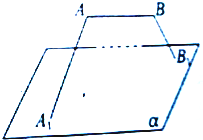 线段AB与平面α平行,α的斜线A1A、B1B与α所成的角分别为30°和60°,且∠A1AB=∠B1BA=90°,AB=2,A1B1=4,求AB与平面α的距离.
线段AB与平面α平行,α的斜线A1A、B1B与α所成的角分别为30°和60°,且∠A1AB=∠B1BA=90°,AB=2,A1B1=4,求AB与平面α的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8-π}{4}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{2-π}{2}$ | D. | $\frac{4-π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知平行四边形ABCD与直角梯形ABEF所在的平面互相垂直,且AB=BE=$\frac{1}{2}$AF=1,BE∥AF,AB⊥AF,∠CBA=$\frac{π}{4}$,BC=$\sqrt{2}$,P为DF的中点.
如图,已知平行四边形ABCD与直角梯形ABEF所在的平面互相垂直,且AB=BE=$\frac{1}{2}$AF=1,BE∥AF,AB⊥AF,∠CBA=$\frac{π}{4}$,BC=$\sqrt{2}$,P为DF的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com