
【题目】如图,四棱锥 ![]() 中,底面ABCD为矩形,侧面PAD为正三角形,且平面
中,底面ABCD为矩形,侧面PAD为正三角形,且平面 ![]() ABCD平面, E为PD中点, AD=2.
ABCD平面, E为PD中点, AD=2.
(Ⅰ)求证:平面 ![]() 平面PCD;
平面PCD;
(Ⅱ)若二面角 ![]() 的平面角大小
的平面角大小 ![]() 满足
满足 ![]() ,求四棱锥
,求四棱锥 ![]() 的体积.
的体积.
【答案】解:(Ⅰ)取AD中点为O, BC中点为E,
由侧面PAD为正三角形,且平面 ![]() 平面ABCD知
平面ABCD知 ![]() 平面ABCD,故
平面ABCD,故 ![]() ,
,
又 ![]() ,则
,则 ![]() 平面PAD,所以
平面PAD,所以 ![]() ,
,
又 ![]() ,则
,则 ![]() ,又E是PD中点,则
,又E是PD中点,则 ![]() ,
,
由线面垂直的判定定理知 ![]() 平面PCD,
平面PCD,
又 ![]() 平面AEC,故平面
平面AEC,故平面 ![]() 平面PCD.
平面PCD.
(Ⅱ)
如图所示,建立空间直角坐标系 ![]() ,
,
令AB=a,则 ![]() .
.
由(Ⅰ)知 ![]() 为平面PCE的法向量,
为平面PCE的法向量,
令 ![]() 为平面PAC的法向量,
为平面PAC的法向量,
由于 ![]() 均与n垂直,
均与n垂直,
故 ![]() 即
即 ![]() 解得
解得 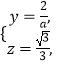
故 ![]() ,由
,由 
 ,解得
,解得 ![]() .
.
故四棱锥 ![]() 的体积
的体积 ![]()
【解析】(1)由平面与平面垂直的性质可得直线与平面垂直,进而得到直线与直线垂直,利用直线与平面垂直的判定定理得到直线与平面垂直,一组相交直线分别垂直于同一平面,故可推出平面与平面垂直。
(2)将立体几何坐标化,通过向量的方法,设出平面法向量,最终求得四棱锥的体积。
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出![]() 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(3)说明此函数图象可由![]() 的图象经怎样的变换得到.
的图象经怎样的变换得到.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块半径为![]() 的正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池
的正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池![]() 和其附属设施,附属设施占地形状是等腰
和其附属设施,附属设施占地形状是等腰![]() ,其中
,其中![]() 为圆心,
为圆心, ![]() 在圆的直径上,
在圆的直径上, ![]() 在半圆周上,如图.
在半圆周上,如图.
(1)设![]() ,征地面积为
,征地面积为![]() ,求
,求![]() 的表达式,并写出定义域;
的表达式,并写出定义域;
(2)当![]() 满足
满足![]() 取得最大值时,开发效果最佳,求出开发效果最佳的角
取得最大值时,开发效果最佳,求出开发效果最佳的角![]() 的值,
的值,
求出![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C: ![]() ,点
,点 ![]() 在x轴的正半轴上,过点M的直线
在x轴的正半轴上,过点M的直线 ![]() 与抛物线C相交于A,B两点,O为坐标原点.
与抛物线C相交于A,B两点,O为坐标原点.
(1)若 ![]() ,且直线
,且直线 ![]() 的斜率为1,求以AB为直径的圆的方程;
的斜率为1,求以AB为直径的圆的方程;
(2)是否存在定点M,使得不论直线 ![]() 绕点M如何转动,
绕点M如何转动, ![]() 恒为定值?
恒为定值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (e为自然对数的底).若函数g(x)=f(x)﹣kx恰好有两个零点,则实数k的取值范围是( )
(e为自然对数的底).若函数g(x)=f(x)﹣kx恰好有两个零点,则实数k的取值范围是( )
A.(1,e)
B.(e,10]
C.(1,10]
D.(10,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有a个黑球和b个白球,随机地每次从中取出一球,每次取后不放回,记事件A为“直到第k次才取到黑球”,其中1≤k≤b;事件B为“第7次取出的球恰好是黑球”,其中1≤k≤b。
(Ⅰ)若a=5,b=3,k=2,求事件A发生的概率;
(Ⅱ)判断事件B发生的概率是否随k取值的变化而变化?并说明理由;
(Ⅲ)比较a=5,b=9时事件A发生的概率与a=5,b=10时事件A发生的概率的大小,并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 是两条不同的直线,
是两条不同的直线, ![]() ,
, ![]() ,
, ![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
, ![]() ,则
,则![]() ②若
②若![]() ,
, ![]() ,
, ![]() ,则
,则![]()
③若![]() ,
, ![]() ,则
,则![]() ④若
④若![]() ,
, ![]() ,则
,则![]()
其中正确命题的序号是( ).
A. ①和② B. ②和③ C. ③和④ D. ①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018河南南阳市一中上学期第三次月考】已知点![]() 为坐标原点,
为坐标原点, ![]() 是椭圆
是椭圆![]() 上的两个动点,满足直线
上的两个动点,满足直线![]() 与直线
与直线![]() 关于直线
关于直线![]() 对称.
对称.
(I)证明直线![]() 的斜率为定值,并求出这个定值;
的斜率为定值,并求出这个定值;
(II)求![]() 的面积最大时直线
的面积最大时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com