
【题目】已知函数![]() .
.
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出![]() 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(3)说明此函数图象可由![]() 的图象经怎样的变换得到.
的图象经怎样的变换得到.

【答案】(1)见解析(2)见解析(3)见解析
【解析】分析:(1)先根据配角公式化函数为基本三角函数形式,列表,求点坐标,描点连线即得图像,(2)根据图像或正弦函数性质求![]() 的周期、振幅、初相、对称轴;(3)根据解析式关系,通过上下左右平移,以及伸缩变换得结果.注意平移单位是相对x而言.
的周期、振幅、初相、对称轴;(3)根据解析式关系,通过上下左右平移,以及伸缩变换得结果.注意平移单位是相对x而言.
详解:
解:(1)![]() =3sin(
=3sin(![]() )+3
)+3
列表
x |
|
|
|
|
|
| 0 |
|
|
|
|
| 3 | 6 | 3 | 0 | 3 |
描点作图
(2)周期T=![]() ,振幅A=3,初相
,振幅A=3,初相![]() ,
,
由![]() ,得
,得![]() 即为对称轴;
即为对称轴;
(3)①由![]() 的图象上各点向左平移
的图象上各点向左平移![]() 个长度单位,得
个长度单位,得![]() 的图象;
的图象;
②由![]() 的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得
的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得![]() 的图象;
的图象;
③由![]() 的图象上各点的纵坐标伸长为原来的3倍(横坐标不变),得
的图象上各点的纵坐标伸长为原来的3倍(横坐标不变),得![]() 的图象;
的图象;
④由![]() 的图象上各点向上平移3个长度单位,得
的图象上各点向上平移3个长度单位,得![]() +3的图象.
+3的图象.


科目:高中数学 来源: 题型:
【题目】某种商品在30天内每克的销售价格![]() (元)与时间
(元)与时间![]() 的函数图像是如图所示的两条线段
的函数图像是如图所示的两条线段![]() ,
,![]() (不包含
(不包含![]() ,
,![]() 两点);该商品在 30 天内日销售量
两点);该商品在 30 天内日销售量![]() (克)与时间
(克)与时间![]() (天)之间的函数关系如下表所示.
(天)之间的函数关系如下表所示.
第 | 5 | 1 5 | 2 0 | 3 0 |
销售量 | 3 5 | 2 5 | 2 0 | 1 0 |
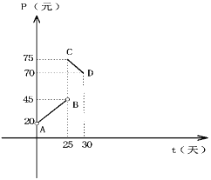
(1)根据提供的图象,写出该商品每克销售的价格![]() (元)与时间
(元)与时间![]() 的函数关系式;
的函数关系式;
(2)根据表中数据写出一个反映日销售量![]() 随时间
随时间![]() 变化的函数关系式;
变化的函数关系式;
(3)在(2)的基础上求该商品的日销售金额的最大值,并求出对应的![]() 值.
值.
(注:日销售金额=每克的销售价格×日销售量)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() .
.
(1)求函数 ![]() 的最大值;
的最大值;
(2)对于任意 ![]() ,且
,且 ![]() ,是否存在实数
,是否存在实数 ![]() ,使
,使 ![]() 恒成立,若存在求出
恒成立,若存在求出 ![]() 的范围,若不存在,说明理由;
的范围,若不存在,说明理由;
(3)若正项数列 ![]() 满足
满足 ![]() ,且数列
,且数列 ![]() 的前
的前 ![]() 项和为
项和为 ![]() ,试判断
,试判断 ![]() 与
与 ![]() 的大小,并加以证明.
的大小,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() ;③若
;③若![]() ,则
,则![]() ;④若
;④若![]() ,
, ![]() 且
且![]() ,则
,则![]() 的最小值为9;其中正确命题的序号是______(将你认为正确的命题序号都填上).
的最小值为9;其中正确命题的序号是______(将你认为正确的命题序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A.命题“若 ![]() ,则
,则 ![]() ”的逆命题为“若
”的逆命题为“若 ![]() ,则
,则 ![]() ”
”
B.对于命题 ![]() ,使得
,使得 ![]() ,则
,则 ![]() ,则
,则 ![]()
C.“ ![]() ”是“
”是“ ![]() ”的充分不必要条件
”的充分不必要条件
D.若 ![]() 为假命题,则
为假命题,则 ![]() 均为假命题
均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥 ![]() 中,底面ABCD为矩形,侧面PAD为正三角形,且平面
中,底面ABCD为矩形,侧面PAD为正三角形,且平面 ![]() ABCD平面, E为PD中点, AD=2.
ABCD平面, E为PD中点, AD=2.
(Ⅰ)求证:平面 ![]() 平面PCD;
平面PCD;
(Ⅱ)若二面角 ![]() 的平面角大小
的平面角大小 ![]() 满足
满足 ![]() ,求四棱锥
,求四棱锥 ![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次“汉马”(武汉马拉松比赛的简称)全程比赛中,50名参赛选手(24名男选手和26名女选手)的成绩(单位:分钟)分别为数据![]() (成绩不为0).
(成绩不为0).
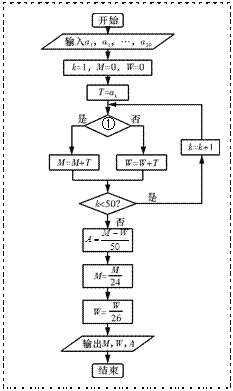
(Ⅰ)24名男选手成绩的茎叶图如图⑴所示,若将男选手成绩由好到差编为1~24号,再用系统抽样方法从中抽取6人,求其中成绩在区间![]() 上的选手人数;
上的选手人数;

(Ⅱ)如图⑵所示的程序用来对这50名选手的成绩进行统计.为了便于区别性别,输入时,男选手的成绩数据用正数,女选手的成绩数据用其相反数(负数),请完成图⑵中空白的判断框①处的填写,并说明输出数值![]() 和
和![]() 的统计意义.
的统计意义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com