解:(Ⅰ)F(x)=f(x)+g(x)=2x
2+ax+lnx,
∴
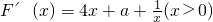
,又F(x)在x=1处取得极小值
∴F'(1)=4+a+1=0,∴a=-5,F(x)=2x
2-5x+lnx
∴
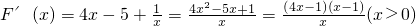
| x |  |  | 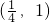 | 1 | (1,+∞) |
| F'(x) | + | 0 | - | 0 | + |
| F(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
∴F(x)的极大值为
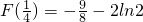
.
(Ⅱ)由F(x)在区间

上是增函数得
当
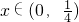
时,
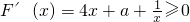
恒成立,设
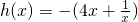
则a≥h(x),又
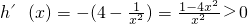
,∴h(x)在

上是增函数,
∴a≥h(x)
max,
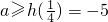
,即实数a的取值范围为[-5,+∞).
(Ⅲ)当a=3时,f(x)=2x
2+3x,g(x)=lnx,∴f'(x)=4x+3,
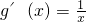
.
设直线l与曲线y=f(x)和y=g(x)都相切,切点分别为A(x
1,y
1),B(x
2,y
2)
则y
1=2x
12+3x
1,y
2=lnx
2∴l:y-(2x
12+3x
1)=(4x
1+3)(x-x
1),即y=(4x
1+3)x-2x
12又l过点B(x
2,y
2)且f'(x)=g'(x),∴y
2=(4x
1+3)x
2-2x
12且
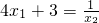
∴lnx
2=(4x
1+3)x
2-2x
12,∴-ln(4x
1+3)=1-2x
12方程2x
12-ln(4x
1+3)-1=0有根,设φ(x)=2x
2-ln(4x+3)-1,
则
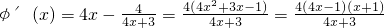
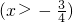
当
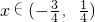
时,φ'(x)<0,φ(x)是减函数,
当
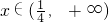
时,φ'(x)>0,φ(x)是增函数,
∴
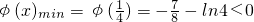
.
又当
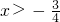
且x趋向于

时,φ(x)趋向于+∞,
∴
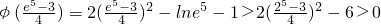
,
∴φ(x)在区间
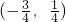
、
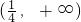
上各有一个根.
∴与曲线y=f(x)和y=g(x)都相切的直线存在,有2条.
分析:(Ⅰ)求出F'(x),因为函数在x=1处取得极值,即得到F'(1)=0,代入求出a与b得到函数解析式,然后讨论利用x的取值范围讨论函数的增减性,得到F(x)极大值;
(Ⅱ)对函数F(x)=2x
2+ax+lnx进行求导,转化成F′(x)在(0,

)上恒有f′(x)≥0,求出参数a的取值范围
(Ⅲ)对于存在性问题,可先假设存在,即假设存在,使直线m既是曲线y=f(x)的切线,又是曲线y=g(x)的切线,再利用导数的几何意义,求出曲线y=g(x)的切线和曲线y=f(x)的切线,若出现矛盾,则说明假设不成立,即不存在;否则存在.
点评:本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于中档题.

 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;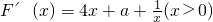 ,又F(x)在x=1处取得极小值
,又F(x)在x=1处取得极小值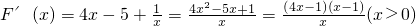


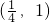
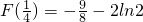 .
. 上是增函数得
上是增函数得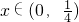 时,
时,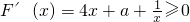 恒成立,设
恒成立,设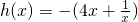
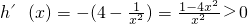 ,∴h(x)在
,∴h(x)在 上是增函数,
上是增函数,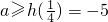 ,即实数a的取值范围为[-5,+∞).
,即实数a的取值范围为[-5,+∞).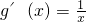 .
.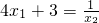
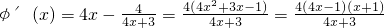
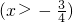
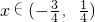 时,φ'(x)<0,φ(x)是减函数,
时,φ'(x)<0,φ(x)是减函数,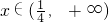 时,φ'(x)>0,φ(x)是增函数,
时,φ'(x)>0,φ(x)是增函数,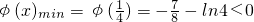 .
.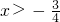 且x趋向于
且x趋向于 时,φ(x)趋向于+∞,
时,φ(x)趋向于+∞,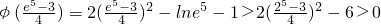 ,
,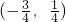 、
、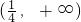 上各有一个根.
上各有一个根. )上恒有f′(x)≥0,求出参数a的取值范围
)上恒有f′(x)≥0,求出参数a的取值范围
