
分析 (1)求得f(x)的导数,由导数大于0,可得增区间;导数小于0,可得减区间,即可得到最小值.求得端点处的函数值,可得最大值;
(2)求出f(x)的导数,讨论a=0,a>0,a<0,判断单调性,可得最小值,解不等式即可得到所求a的范围.
解答 解:(1)当a=1时,$f(x)=\frac{2}{x}-2+2lnx$,其定义域为(0,+∞),
则f′(x)=-$\frac{2}{{x}^{2}}$+$\frac{2}{x}$=$\frac{2(x-1)}{{x}^{2}}$,
令f′(x)<0,得0<x<1;令f′(x)>0,得x>1,
所以函数f(x)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,
所以函数f(x)在区间$[\frac{1}{2},2]$上的最小值为f(1)=0;
又$f(\frac{1}{2})=2-2ln2$,f(2)=-1+2ln2,且$f(2)-f(\frac{1}{2})=4ln2-3=ln16-3<0$,
所以$f(2)<f(\frac{1}{2})$,
所以函数f(x)在区间$[\frac{1}{2},2]$上的最大值为$f(\frac{1}{2})=2-2ln2$.
(2)${f^'}(x)=-\frac{2}{x^2}+\frac{2a}{x}=\frac{2ax-2}{x^2}$,
①当a>0时,令f′(x)<0,得$x<\frac{1}{a}$;令f′(x)>0,得$x>\frac{1}{a}$,
所以函数f(x)在区间$(0,\frac{1}{a})$上单调递减,在区间$(\frac{1}{a},+∞)$上单调递增.
所以函数f(x)在区间(0,+∞)上的最小值为$f(\frac{1}{a})$;
若f(x)>-2恒成立,则$f(\frac{1}{a})>-2$,即2a-2-2alna>-2,即2a(1-lna)>0,
又因为a>0,所以1-lna>0,解得a<e,所以0<a<e;
②当a=0时,$f(x)=\frac{2}{x}-2>-2$恒成立,所以a=0符合题意;
③当a<0时,令f′(x)<0,得$x>\frac{1}{a}$;令f′(x)>0,得$x<\frac{1}{a}$,
所以函数f(x)在区间$(0,\frac{1}{a})$上单调递增,在区间$(\frac{1}{a},+∞)$上单调递减.
数形结合易知,一定存在某个x0>0,使得在区间(x0,+∞)上,
函数$y=\frac{2}{x}$的图象在函数y=-2alnx的图象的下方,
即满足$\frac{2}{x}<-2alnx$,即$\frac{2}{x}-2+2alnx<-2$,即f(x)<-2.
所以f(x)>-2不恒成立,故a<0不符合题意,舍去;
综上,实数a的取值范围是[0,e).
点评 本题考查导数的运用:求单调区间、极值和最值,考查不等式恒成立问题的解法,注意运用分类讨论的思想方法和转化思想,运用函数的单调性,考查化简整理的运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
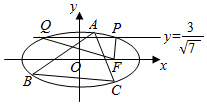 已知右焦点为F的椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>$\sqrt{3}$)与直线y=$\frac{3}{\sqrt{7}}$相交于P,Q两点,且PF⊥QF.
已知右焦点为F的椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>$\sqrt{3}$)与直线y=$\frac{3}{\sqrt{7}}$相交于P,Q两点,且PF⊥QF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
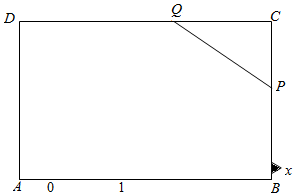 在矩形ABCD中,AB=5,BC=2,现截去一个△PCQ,使P、Q分别落在边BC、CD上,且△PCQ的周长为8,设PC=x∈(0,2],CQ=t.
在矩形ABCD中,AB=5,BC=2,现截去一个△PCQ,使P、Q分别落在边BC、CD上,且△PCQ的周长为8,设PC=x∈(0,2],CQ=t.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 从气球A上测得正前方的河流的两岸B,C的俯角分别为α,β,如果这时气球的高是100米,则河流的宽度BC为( )
从气球A上测得正前方的河流的两岸B,C的俯角分别为α,β,如果这时气球的高是100米,则河流的宽度BC为( )| A. | $\frac{100(tanβ-tanα)}{tanαtanβ}$ | B. | $\frac{100tanαtanβ}{tanα-tanβ}$ | ||
| C. | $\frac{100(tanα+tanβ)}{tanαtanβ}$ | D. | $\frac{100tanαtanβ}{tanα+tanβ}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | a>c>b | C. | c>b>a | D. | c>a>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com