
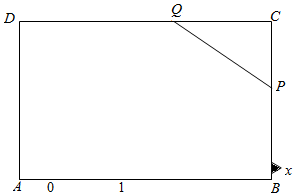
 在矩形ABCD中,AB=5,BC=2,现截去一个△PCQ,使P、Q分别落在边BC、CD上,且△PCQ的周长为8,设PC=x∈(0,2],CQ=t.
在矩形ABCD中,AB=5,BC=2,现截去一个△PCQ,使P、Q分别落在边BC、CD上,且△PCQ的周长为8,设PC=x∈(0,2],CQ=t.分析 (1)根据题意和图象,利用勾股定理求出PQ,由△PCQ的周长为8列出方程,化简可得t=f(x)的表达式;
(2)由(1)和三角形、矩形的面积公式,表示出矩形ABCD剩下部分面积,求导化简后,利用二次函数的性质、导数的符号判断出函数的单调性,即可求出矩形ABCD剩下部分面积的最小值.
解答 解:(1)∵PC=x∈(0,2],CQ=t,(x>0、t>0)
∴在RT△PCQ中,由勾股定理得,
PQ=$\sqrt{C{P}^{2}+C{Q}^{2}}$=$\sqrt{{t}^{2}+{x}^{2}}$,
∵△PCQ的周长为8,∴x+t+$\sqrt{{t}^{2}+{x}^{2}}$=8,
化简可得,32=8x+8t-xt,即(8-x)t=32-8x,
故t=f(x)=$\frac{32-8x}{8-x}$,(0≤x≤2);
(2)由(1)得,
矩形ABCD剩下部分面积S=$5×2-\frac{1}{2}×t×x$
=10-$\frac{4x(4-x)}{8-x}$=$\frac{2(2{x}^{2}-13x+40)}{8-x}$,
∴S′(x)=$2•\frac{(2{x}^{2}-13x+40)′(8-x)-(2{x}^{2}-13x+40)(8-x)′}{(8-x)^{2}}$
=$4•\frac{-{x}^{2}+16x-32}{{(8-x)}^{2}}$=$4•\frac{-{(x-8)}^{2}+32}{{(8-x)}^{2}}$,
∵0≤x≤2,∴当x=2时,$4•\frac{-{(x-8)}^{2}+32}{{(8-x)}^{2}}$取到最大值是$-\frac{4}{9}<0$,
∴当x∈[0,2]时,S′(x)<0,则S(x)在[0,2]上递减,
当x=2时,S(x)取到最小值是$\frac{22}{3}$,
即矩形ABCD剩下部分面积的最小值是$\frac{22}{3}$.
点评 本题考查了函数解析式的求解,二次函数的性质,导数与函数单调性、最值的关系,考查化简、变形能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{e}$-2 | B. | 1-2e | C. | 1-e | D. | 2-$\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
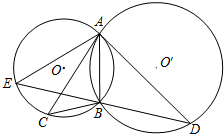 如图,⊙O和⊙O′相交于A,B两点,过A作两圆的切线分别交两圆于C,D两点,连结DB并延长交⊙O于点E,已知AC=BD=3.
如图,⊙O和⊙O′相交于A,B两点,过A作两圆的切线分别交两圆于C,D两点,连结DB并延长交⊙O于点E,已知AC=BD=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,$\frac{7}{6}π}$) | B. | (2,-$\frac{7}{6}π}$) | C. | (-2,-$\frac{11π}{6}}$) | D. | (-2,$\frac{13}{6}π}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com