
【题目】设a<0,(3x2+a)(2x+b)≥0在(a,b)上恒成立,则b﹣a的最大值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:∵(3x2+a)(2x+b)≥0在(a,b)上恒成立,
∴3x2+a≥0,2x+b≥0或3x2+a≤0,2x+b≤0,
①若2x+b≥0在(a,b)上恒成立,则2a+b≥0,即b≥﹣2a>0,
此时当x=0时,3x2+a=a≥0不成立,
②若2x+b≤0在(a,b)上恒成立,则2b+b≤0,即b≤0,
若3x2+a≤0在(a,b)上恒成立,则3a2+a≤0,即﹣ ![]() ≤a≤0,
≤a≤0,
故b﹣a的最大值为 ![]() ,
,
故选:A
【考点精析】掌握二次函数的性质和基本不等式是解答本题的根本,需要知道当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减;基本不等式:
上递减;基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() .
.


科目:高中数学 来源: 题型:
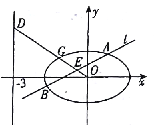
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,如图所示,斜率为
,如图所示,斜率为![]() 且不过原点的直线
且不过原点的直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,射线
,射线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求![]() 的最小值;
的最小值;
(2)若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数 ![]() 的图象,只要将函数y=sin2x的图象( )
的图象,只要将函数y=sin2x的图象( )
A.向右平移 ![]() 个单位长度
个单位长度
B.向左平移 ![]() 个单位长度
个单位长度
C.向右平移 ![]() 个单位长度
个单位长度
D.向左平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们称满足: ![]() (
(![]() )的数列
)的数列![]() 为“
为“![]() 级梦数列”.
级梦数列”.
(1)若![]() 是“
是“![]() 级梦数列”且
级梦数列”且![]() .求:
.求: ![]() 和
和![]() 的值;
的值;
(2)若![]() 是“
是“![]() 级梦数列”且满足
级梦数列”且满足![]() ,
, ![]() ,求
,求![]() 的最小值;
的最小值;
(3)若![]() 是“0级梦数列”且
是“0级梦数列”且![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() .证明:
.证明: ![]() (
(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x+x,g(x)=x3+x,h(x)=log3x+x的零点依次为a,b,c,则( )
A.c<b<a
B.a<b<c
C.c<a<b
D.b<a<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块半圆形空地,开发商计划建一个矩形游泳池![]() 及其矩形附属设施
及其矩形附属设施![]() ,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为
,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为![]() ,半径为
,半径为![]() ,矩形的一边
,矩形的一边![]() 在直径上,点
在直径上,点![]() 、
、![]() 、
、![]() 、
、![]() 在圆周上,
在圆周上,![]() 、
、![]() 在边
在边![]() 上,且
上,且![]() ,设
,设![]() .
.
(1)记游泳池及其附属设施的占地面积为![]() ,求
,求![]() 的表达式;
的表达式;
(2)怎样设计才能符合园林局的要求?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,其中
,其中![]() 为常数;
为常数;
(1)若![]() ,且
,且![]() 是奇函数,求
是奇函数,求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,函数
,函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的最大值;
的最大值;
(3)若![]() ,在
,在![]() 上存在
上存在![]() 个点
个点![]()
![]() ,满足
,满足![]() ,
, ![]() ,
,
![]() ,使得
,使得![]() ,
,
求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学在5次考试中的数学成绩用茎叶图表示如图,中间一列的数字表示数学成绩的十位数字,两边的数字表示数学成绩的个位数字,若甲、乙两人的平均成绩分别是 ![]() ,
, ![]() ,则下列说法正确的是( )
,则下列说法正确的是( ) 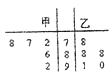
A.![]() ,甲比乙成绩稳定
,甲比乙成绩稳定
B.![]() ,乙比甲成绩稳定
,乙比甲成绩稳定
C.![]() ,甲比乙成绩稳定
,甲比乙成绩稳定
D.![]() ,乙比甲成绩稳定
,乙比甲成绩稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com