
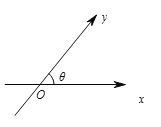
【题目】如图,数轴![]() ,
,![]() 的交点为
的交点为![]() ,夹角为
,夹角为![]() ,与
,与![]() 轴、
轴、![]() 轴正向同向的单位向量分别是
轴正向同向的单位向量分别是![]() ,
,![]() .由平面向量基本定理,对于平面内的任一向量
.由平面向量基本定理,对于平面内的任一向量![]() ,存在唯一的有序实数对
,存在唯一的有序实数对![]() ,使得
,使得![]() ,我们把
,我们把![]() 叫做点
叫做点![]() 在斜坐标系
在斜坐标系![]() 中的坐标(以下各点的坐标都指在斜坐标系
中的坐标(以下各点的坐标都指在斜坐标系![]() 中的坐标).
中的坐标).
(1)若![]() ,
,![]() 为单位向量,且
为单位向量,且![]() 与
与![]() 的夹角为
的夹角为![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若![]() ,点
,点![]() 的坐标为
的坐标为![]() ,求向量
,求向量![]() 与
与![]() 的夹角;
的夹角;
(3)若![]() ,求过点
,求过点![]() 的直线
的直线![]() 的方程,使得原点
的方程,使得原点![]() 到直线
到直线![]() 的距离最大.
的距离最大.
科目:高中数学 来源: 题型:
【题目】在合作学习小组的一次活动中,甲、乙、丙、丁、戊五位同学被随机地分配承担![]() ,
,![]() ,
,![]() ,
,![]() 四项不同的任务,每个同学只能承担一项任务.
四项不同的任务,每个同学只能承担一项任务.
(1)若每项任务至少安排一位同学承担,求甲、乙两人不同时承担同一项任务的概率;
(2)设这五位同学中承担任务![]() 的人数为随机变量
的人数为随机变量![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙、丙三个乒乓球协会分别选派3,1,2名运动员参加某次比赛,甲协会运动员编号分别为![]() ,
,![]() ,
,![]() ,乙协会编号为
,乙协会编号为![]() ,丙协会编号分别为
,丙协会编号分别为![]() ,
,![]() ,若从这6名运动员中随机抽取2名参加双打比赛.
,若从这6名运动员中随机抽取2名参加双打比赛.
(1)用所给编号列出所有可能抽取的结果;
(2)求丙协会至少有一名运动员参加双打比赛的概率;
(3)求参加双打比赛的两名运动员来自同一协会的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆上的点到右焦点
,椭圆上的点到右焦点![]() 的距离的最大值为3.
的距离的最大值为3.
(1)求椭圆![]() 的方程;
的方程;
(2)若过椭圆![]() 的右焦点
的右焦点![]() 作倾斜角不为零的直线
作倾斜角不为零的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,设线段
,设线段![]() 的垂直平分线在
的垂直平分线在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一次全市高中男生身高统计调查数据显示:全市100000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160 cm和184 cm之间,将测量结果按如下方式分成6组:第1组[160,164),第2组[164,168),…,第6组[180,184],如图是按上述分组方法得到的频率分布直方图.
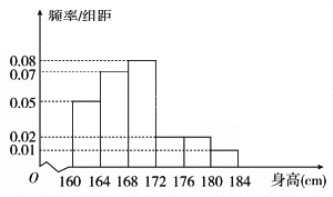
(1)由频率分布直方图估计该校高三年级男生平均身高状况;
(2)求这50名男生身高在172 cm以上(含172 cm)的人数;
(3)在这50名男生身高在172 cm以上(含172 cm)的人中任意抽取2人,将该2人中身高排名(从高到低)在全市前130名的人数记为ξ,求ξ的数学期望.
参考数据:若ξ~N(μ,σ2),则P(μ-σ<ξ≤μ+σ)=0.6826,P(μ-2σ<ξ≤μ+2σ)=0.9544,P(μ-3σ<ξ≤μ+3σ)=0.9974.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且椭圆上一点
,且椭圆上一点![]() 的坐标为
的坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以线段
两点,且以线段![]() 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数,
为自然对数的底数,![]() 。
。
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值;
的值;
(Ⅱ)若![]() ,问函数
,问函数![]() 有无极值点?若有,请求出极值点的个数;若没有,请说明理由。
有无极值点?若有,请求出极值点的个数;若没有,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com