练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     （理）在棱长为1的正方体ABCD—A1B1C1D1中，M和N分别为A1B1和BB1的中点，则异面直线AM与CN所成角的余弦值为         （    ）

        A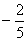． B．    C．   D．

    （文）

        A．cosx B．－cosx   C．sinx D．－sinx

     

    【答案】

     D（B） 

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （08年长沙一中一模理）某种游戏中，黑、黄两个“电子狗”从棱长为1的正方体的顶点A出发沿棱向前爬行，每爬完一条棱称为“爬完一段”。黑“电子狗”爬行的路线是，黄“电子狗”爬行的路线是它们都遵循如下规则：所爬行的第段与第段所在直线必须是异面直线（其中是正整数）.设黑“电子狗”爬完2008段、黄“电子狗”爬完2007段后知自停止在正方体的某个顶点处，这时黑、黄“电了狗”间的距离是（    ）

           A．0                            B．1                            C．                       D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （06年浙江卷理）正四面体ABCD的棱长为1，棱AB∥平面α，则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是　　　.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （06年湖南卷理）棱长为2的正四面体的四个顶点都在同一个球面上, 若过该球球心的一个截面如图1,则图中三角形(正四面体的截面)的面积是                 

    A．          B．           C．           D． 

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年鄂尔多斯市一模理） 如图，在各棱长都为2的正三棱柱ABC―A1B1C1中，的重心.

       （1）求证：DG//平面ABC；

       （2）求二面角B―AG―C的大小；

       （3）求点B1到平面AGC的距离.

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

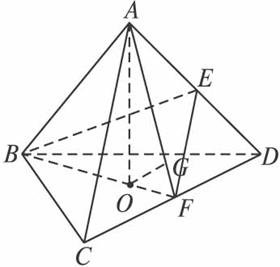
    如图,棱长为1的正四面体ABCD中,E、F分别是棱AD、CD的中点,O是点A在平面BCD内的射影.

    (1)求直线EF与直线BC所成角的大小;

    (2)求点O到平面ACD的距离;

    (3)(理)求二面角ABEF的大小.

    (文)求二面角CBFE的大小.

    查看答案和解析>>

    同步练习册答案