
如图,梯形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=2AB=4,E,F分别在线段BC,AD上,EF∥AB.将四边形ABEF沿EF折起,连接AD,AC.
(Ⅰ)若BE=3,在线段AD上一点取一点P,使 ,求证:CP∥平面ABEF;
,求证:CP∥平面ABEF;
(Ⅱ)若平面ABEF⊥平面EFDC,且线段FA,FC,FD的长成等比数列,求二面角E-AC-F的大小.
 |
 解:(Ⅰ)证法一:在梯形ABCD中,
解:(Ⅰ)证法一:在梯形ABCD中,
AD∥BC, EF∥AB ,BE=3,∴AF=3,
又AD=6,BC=4,∴EC=1,FD=3, 1分
在线段AF上取点Q,使 ,连接
,连接 , 2分
, 2分
∵ ,∴
,∴ ,
,
 ∵
∵ ,∴
,∴ , 3分
, 3分
∴四边形ECPQ为平行四边形,∴ , 4分
, 4分
∵ 平面ABEF,
平面ABEF, 平面ABEF,∴CP∥平面ABEF. 5分
平面ABEF,∴CP∥平面ABEF. 5分
证法二:同证法一,EC=1,FD=3, 1分
延长DC交FE的延长线于点M,连接 ,则
,则 , 2分
, 2分
∵ ,∴
,∴ , 4分
, 4分
∵ 平面ABEF,
平面ABEF, 平面ABEF,∴CP∥平面ABEF. 5分
平面ABEF,∴CP∥平面ABEF. 5分
 证法三:同证法一,EC=1,FD=3, 1分
证法三:同证法一,EC=1,FD=3, 1分
在线段DF上取点R,使 ,连接PR,CR,
,连接PR,CR,
∵ ,∴
,∴ ,
,
∵ 平面ABEF,
平面ABEF, 平面ABEF,∴PR∥平面ABEF; 2分
平面ABEF,∴PR∥平面ABEF; 2分
∵ , ∴
, ∴
∵ , ∴四边形ECRF为平行四边形,∴
, ∴四边形ECRF为平行四边形,∴ ,
,
∵ 平面ABEF,
平面ABEF, 平面ABEF,∴CR∥平面ABEF; 3分
平面ABEF,∴CR∥平面ABEF; 3分
∵ ,∴平面
,∴平面 平面
平面 , 4分
, 4分
∵ 平面PRC,∴CP∥平面ABEF. 5分
平面PRC,∴CP∥平面ABEF. 5分
(Ⅱ)解法一:在梯形ABCD中,AB⊥AD,AD∥BC,∴EF⊥AF, EF⊥FD,
∵平面ABEF⊥平面EFDC,平面ABEF 平面EFDC=
平面EFDC= ,AF
,AF 平面EFDC,
平面EFDC,
∴AF⊥平面EFDC, 6分
设 ,
,
∵EF=BA=2,∴ ,
,
∴ , 7分
, 7分
∵线段AF,FC,FD的长成等比数列,∴ ,
,
 ,化简得
,化简得 ,
,
∴ 或
或 (舍), 9分
(舍), 9分
以F为原点,FE,FD,FA分别为 轴建立空间直角坐标系,如图,
轴建立空间直角坐标系,如图,
 则
则 ,
, ,
, ,
, ,
, , 10分
, 10分
∴ ,
, ,
,
设 是平面ACE的一个法向量,
是平面ACE的一个法向量,
则 ,即
,即 ,
,
取 ,则
,则 ,∴
,∴ ; 11分
; 11分
又 ,
, ,
,
设 是平面ACF的一个法向量,
是平面ACF的一个法向量,
 则
则 ,即
,即 ,
,
取 ,则
,则 ∴
∴ ; 12分
; 12分
∴ ,
,
∵ 二面角E-AC-F为锐角, ∴二面角E-AC-F为 . 13分
. 13分
解法二:同解法一得 或
或 (舍), 9分
(舍), 9分
 ,
,
∵ ,∴
,∴ ,
,
设点G为FC的中点,连接 ,则
,则 , 10分
, 10分
∵AF⊥平面EFDC, 平面AFC,∴平面AFC
平面AFC,∴平面AFC 平面EFDC,
平面EFDC,
∵平面AFC 平面EFDC=
平面EFDC= ,∴EG⊥平面AFC,
,∴EG⊥平面AFC,
∵ 平面AFC , ∴EG⊥AC, 11分
平面AFC , ∴EG⊥AC, 11分
过G作GH⊥AC交AC于H,连接EH,
∵EG GH=G, ∴AC⊥平面EGH,
GH=G, ∴AC⊥平面EGH,
∵EH 平面EGH,∴AC⊥EH,
平面EGH,∴AC⊥EH,
∴ 是二面角E-AC-F的平面角, 12分
是二面角E-AC-F的平面角, 12分
在 中,
中, ,
,
在 中,
中, ,∴
,∴ ,
,  ,∴
,∴ ,
,
∵ 为锐角, ∴
为锐角, ∴ ,即二面角E-AC-F为
,即二面角E-AC-F为 . 13分
. 13分


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
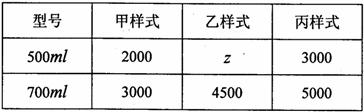
以工厂生产甲、乙、丙三种样式的杯子,每种样式均有500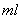 和700
和700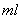 两种型号,某天的产量如右表(单位:个):按分层抽样的方法在这个月生产的杯子中抽取100个,其中有甲样式杯子25个.
两种型号,某天的产量如右表(单位:个):按分层抽样的方法在这个月生产的杯子中抽取100个,其中有甲样式杯子25个.
(1)求 的值;
的值;
(2)用分层抽样的方法在甲样式杯子中抽取一个容量为5的样本,从这个样本中任取2个杯子,求至少有1个500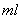 杯子的概率.
杯子的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知曲线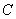 的极坐标方程为
的极坐标方程为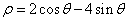 .以极点为原点,极轴为
.以极点为原点,极轴为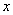 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程为
的参数方程为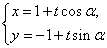 (
(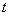 为参数).
为参数).
(Ⅰ)判断直线 与曲线
与曲线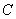 的位置关系,并说明理由;
的位置关系,并说明理由;
(Ⅱ)若直线 和曲线
和曲线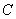 相交于
相交于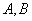 两点,且
两点,且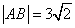 ,求直线
,求直线 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com