
分析 ⊙C:x2+y2+2x-4y+3=0,化为标准方程,求出圆心C,半径r.设P(x,y).由切线的性质可得:CM⊥PM,利用|PM|=|PO|,可得2x1-4y1+3=0.要使|PM|最小,只要|PO|最小即可.
解答 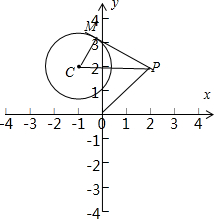 解:如图所示,⊙C:x2+y2+2x-4y+3=0化为(x+1)2+(y-2)2=2,圆心C(-1,2),半径r=$\sqrt{2}$.
解:如图所示,⊙C:x2+y2+2x-4y+3=0化为(x+1)2+(y-2)2=2,圆心C(-1,2),半径r=$\sqrt{2}$.
因为|PM|=|PO|,
所以|PO|2+r2=|PC|2(C为圆心,r为圆的半径),
所以x12+y12+2=(x1+1)2+(y1-2)2,即2x1-4y1+3=0.要使|PM|最小,只要|PO|最小即可.
当直线PO垂直于直线2x-4y+3=0时,即直线PO的方程为2x+y=0时,|PM|最小,此时P点即为两直线的交点,得P点坐标(-$\frac{3}{10}$,$\frac{3}{5}$).
故答案为:(-$\frac{3}{10}$,$\frac{3}{5}$).
点评 本题考查了圆的切线的性质、勾股定理、两点之间的距离公式,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com