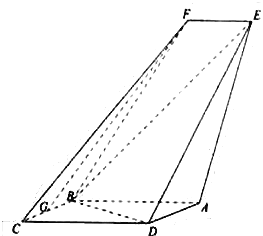
【题目】如图，四边形是平行四边形，平面⊥平面，，，，，，，．

(Ⅰ)求证：平面；

(Ⅱ)求直线与平面所成角的正弦值.

参考答案：

【答案】（1）见解析；（2）直线与平面所成角的正弦值为.

【解析】

（1）利用中位线定理，先证明四边形是平行四边形，可得，再根据线面平行的判定定理即可证明；(2) 先判断出直线与平面所成角即为直线与平面所成角, 过点作于点，连接，又可证明平面，所以直线与平面所成角即为，再根据余弦定理和解直角三角形即可求出结论.

（1）取的中点为，连接，在中，

因为是的中点，所以且，

又因为，所以且，

即四边形是平行四边形，所以，

又平面，平面，

所以平面.

（2）在中，，由余弦定理可，

进而可得，即，

又因为平面平面平面；平面平面，

所以平面.

又因为平面，

所以平面平面.

因为，

所以直线与平面所成角即为直线与平面所成角.

过点作于点，连接，

又因为平面平面，

所以平面，

所以直线与平面所成角即为.

在中，，由余弦定理可得，

所以，因此，

在中，，所以直线与平面所成角的正弦值为．

关闭