
【题目】如图,某自行车手从O点出发,沿折线O﹣A﹣B﹣O匀速骑行,其中点A位于点O南偏东45°且与点O相距20 ![]() 千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°﹣α)(其中sinα=
千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°﹣α)(其中sinα= ![]() ,0°<α<90°)且与点O相距5
,0°<α<90°)且与点O相距5 ![]() 千米(假设所有路面及观测点都在同一水平面上).
千米(假设所有路面及观测点都在同一水平面上).
(1)求该自行车手的骑行速度;
(2)若点O正西方向27.5千米处有个气象观测站E,假定以点E为中心的3.5千米范围内有长时间的持续强降雨.试问:该自行车手会不会进入降雨区,并说明理由.

【答案】(1)![]() (2)会进入
(2)会进入
【解析】
(1)根据余弦定理可求出AC的长,从而可求出自行车的速度;
(2)先根据余弦定理求出cos∠OAC,再根据正弦定理可得OM,再在Rt△EHM中,求出EM的大小,比较后即可得到结论.
(1)由题意知:OA=2![]() ,OC
,OC![]() , ∠AOC=α,sinα=
, ∠AOC=α,sinα=![]() .
.
由于0°<α<90°,
所以![]() .
.
在△AOC中,由余弦定理得
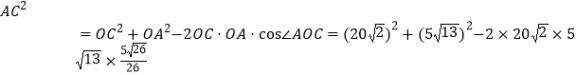
![]() ,
,
所以![]() ,
,
所以该自行车手的行驶速度为![]() (千米/小时).
(千米/小时).
(2)如图,
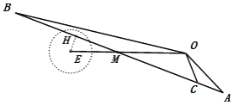
设直线OE与AB相交于点M.
在△AOC中,由余弦定理得
cos∠OAC![]()
从而 sin∠OAC![]() .
.
在△AOM中,由正弦定理得![]() ,
,
所以 ,
,
由于OE=27.5>40=OM,
所以点M位于点O和点E之间,且ME=OE﹣OM=7.5.
过点E作EH AB于点H,
则EH为点E到直线AB的距离.
在Rt△EHM中,EH=EMsin∠EMH=EMsin(45°﹣∠OAC)![]() .
.
所以该自行车手会进入降雨区.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】若![]() 则一定有( )
则一定有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】本题主要考查不等关系。已知![]() ,所以
,所以![]() ,所以
,所以![]() ,故
,故![]() 。故选
。故选![]()
【题型】单选题
【结束】
5
【题目】关于x的不等式ax2+bx+2>0的解集为{x|-1<x<2},则关于x的不等式bx2-ax-2>0的解集为( )
A. {x|-2<x<1} B. {x|x>1或x<-2}
C. {x|x>2或x<-1} D. {x|x<-1或x>1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(1,0,0),B(0,1,0),C(0,0,2).
(1)若![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,求点D的坐标;
,求点D的坐标;
(2)问是否存在实数α,β,使得![]() =α
=α![]() +β
+β![]() 成立?若存在,求出α,β的值;若不存在,说明理由.
成立?若存在,求出α,β的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
如图1,在Rt![]() 中,
中,![]() ,
,![]() .D、E分别是
.D、E分别是![]() 上的点,且
上的点,且![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
(Ⅲ)当![]() 点在何处时,
点在何处时,![]() 的长度最小,并求出最小值.
的长度最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C、D是函数y=sin(ωx+φ)(ω>0,0<φ<![]() )一个周期内的图象上的四个点,如图所示,A(﹣
)一个周期内的图象上的四个点,如图所示,A(﹣![]() , 0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,
, 0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,![]() 在x轴方向上的投影为
在x轴方向上的投影为![]() .
.
(1)求函数f(x)的解析式及单调递减区间;
(2)将函数f(x)的图象向左平移![]() 得到函数g(x)的图象,已知g(α)=
得到函数g(x)的图象,已知g(α)=![]() , α∈(﹣
, α∈(﹣![]() , 0),求g(α+
, 0),求g(α+![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的一个焦点为![]() ,对应于这个焦点的准线方程为
,对应于这个焦点的准线方程为![]()
(1)写出抛物线![]() 的方程;
的方程;
(2)过![]() 点的直线与曲线
点的直线与曲线![]() 交于
交于![]() 两点,
两点,![]() 点为坐标原点,求
点为坐标原点,求![]() 重心
重心![]() 的轨迹方程;
的轨迹方程;
(3)点![]() 是抛物线
是抛物线![]() 上的动点,过点
上的动点,过点![]() 作圆
作圆![]() 的切线,切点分别是
的切线,切点分别是![]() .当
.当![]() 点在何处时,
点在何处时,![]() 的值最小?求出
的值最小?求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x)满足f(x+1)=f(﹣x),当x∈(0,1)时,f(x)=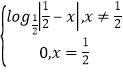 , 则f(x)在区间(1,
, 则f(x)在区间(1,![]() )内是( )
)内是( )
A.增函数且f(x)>0
B.增函数且f(x)<0
C.减函数且f(x)>0
D.减函数且f(x)<0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2,3acosB﹣bcosC=ccosB,点D在线段BC上. 
(1)若∠ADC= ![]() ,求AD的长;
,求AD的长;
(2)若BD=2DC,△ACD的面积为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com