
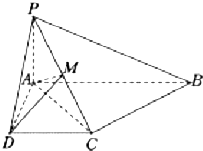
 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,CB=$\sqrt{2}$,AB=2,PA=1.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,CB=$\sqrt{2}$,AB=2,PA=1.分析 (1)由PA⊥平面ABCD,可得PA⊥BC.在△ABC中,由余弦定理可得:AC2=2,因此AC2+BC2=AB2,可得AC⊥BC,即可证明BC⊥平面PAC.
(2)由(1)可得:AD=CD=1,分别以AD,AB,AP为x,y,z轴,建立空间直角坐标系.取平面ACD的法向量$\overrightarrow{n}$=$\overrightarrow{AP}$=(0,0,1).设平面ADM的法向量为$\overrightarrow{m}$=(x,y,z),由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AM}=0}\\{\overrightarrow{m}•\overrightarrow{AD}=0}\end{array}\right.$,可得$\overrightarrow{m}$.利用cos$<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$,即可得出.
解答 (1)证明:∵PA⊥平面ABCD,∴PA⊥BC,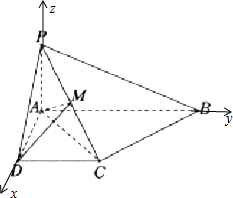
在△ABC中,由余弦定理可得:AC2=${2}^{2}+(\sqrt{2})^{2}$-2×$2×\sqrt{2}×cos4{5}^{°}$=2,
∴AC2+BC2=AB2=4,
∴∠ACB=90°,即AC⊥BC,
又PC∩AC=A,∴BC⊥平面PAC.
(2)解:由(1)可得:AD=CD=1,分别以AD,AB,AP为x,y,z轴,建立空间直角坐标系.
则A(0,0,0),D(1,0,0),P(0,0,1),C(1,1,0),M($\frac{1}{2}$,$\frac{1}{2}$,$\frac{1}{2}$),取平面ACD的法向量$\overrightarrow{n}$=$\overrightarrow{AP}$=(0,0,1).
设平面ADM的法向量为$\overrightarrow{m}$=(x,y,z),$\overrightarrow{AM}$=($\frac{1}{2}$,$\frac{1}{2}$,$\frac{1}{2}$),$\overrightarrow{AD}$=(1,0,0).
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AM}=0}\\{\overrightarrow{m}•\overrightarrow{AD}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{\frac{1}{2}x+\frac{1}{2}y+\frac{1}{2}z=0}\\{x=0}\end{array}\right.$,取$\overrightarrow{m}$=(0,1,-1).
cos$<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{-1}{\sqrt{2}}$,
设二面角M-AD-C的大小为θ,易知θ为锐角.∴cosθ=$\frac{\sqrt{2}}{2}$,θ=45°.
∴二面角M-AD-C的大小为45°.
点评 本题考查了空间位置关系空间角、法向量的应用、向量垂直与数量积的关系、勾股定理,考查了推理能力与计算能力,属于中档题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:解答题
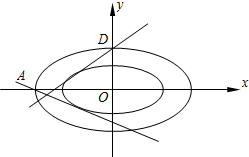 设椭圆E1的长半轴长为a1、短半轴长为b1,椭圆E2的长半轴长为a2、短半轴长为b2,若$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$,则我们称椭圆E1与椭圆E2是相似椭圆.已知椭圆E:$\frac{x^2}{2}$+y2=1,其左顶点为A、右顶点为B.
设椭圆E1的长半轴长为a1、短半轴长为b1,椭圆E2的长半轴长为a2、短半轴长为b2,若$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$,则我们称椭圆E1与椭圆E2是相似椭圆.已知椭圆E:$\frac{x^2}{2}$+y2=1,其左顶点为A、右顶点为B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
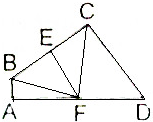
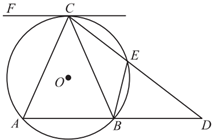 如图,已知CF是圆O的切线,C为切点,弦AB∥CF,E为圆周上一点,CE交AB的延长线于点D,弧$\widehat{AB}$=弧$\widehat{BC}$.求证:
如图,已知CF是圆O的切线,C为切点,弦AB∥CF,E为圆周上一点,CE交AB的延长线于点D,弧$\widehat{AB}$=弧$\widehat{BC}$.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高一 | 高二 | 总计 | |
| 合格人数 | 70 | x | 150 |
| 不合格人数 | y | 20 | 50 |
| 总计 | 100 | 100 | 200 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(k2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,四边形ABCD中,AB=1,AD=7,BC=CD=5,∠BAD=∠BCD=90°.
如图所示,四边形ABCD中,AB=1,AD=7,BC=CD=5,∠BAD=∠BCD=90°.查看答案和解析>>
科目:高中数学 来源:2017届甘肃兰州一中高三9月月考数学(文)试卷(解析版) 题型:选择题
设集合A={x|x>a},集合B={-1,1,2},若A∩B=B,则实数a的取值范围是( )
A.(1,+∞) B.(-∞,1) C.(-1,+∞) D.(-∞,-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com