
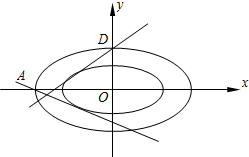
 设椭圆E1的长半轴长为a1、短半轴长为b1,椭圆E2的长半轴长为a2、短半轴长为b2,若$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$,则我们称椭圆E1与椭圆E2是相似椭圆.已知椭圆E:$\frac{x^2}{2}$+y2=1,其左顶点为A、右顶点为B.
设椭圆E1的长半轴长为a1、短半轴长为b1,椭圆E2的长半轴长为a2、短半轴长为b2,若$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$,则我们称椭圆E1与椭圆E2是相似椭圆.已知椭圆E:$\frac{x^2}{2}$+y2=1,其左顶点为A、右顶点为B.分析 (1)利用新定义,通过s>2,0<s<2,分别求出s即可.
(2)求出l1、l2的方程分别为$y={k_1}(x+\sqrt{2})$、y=k2x+1,分别与椭圆方程联立,利用判别式为0,求出|k1|,|k2|,然后推出|k1k2|=$\frac{1}{2}$.
(3)写出椭圆E,椭圆H的方程,求出kAM,kBC,推出向量乘积为-1,即可证明AM⊥BC.
解答 (1)解:显然椭圆E的方程为$\frac{x^2}{2}+{y^2}$=1,
由椭圆E与F相似易得:
当s>2时$\frac{2}{s}=\frac{1}{2}$⇒s=4;…2分
当0<s<2时$\frac{2}{2}=\frac{1}{s}$⇒s=1,…4分
所以s=4或1…4分
(2)证明:易得$A(-\sqrt{2},0),D(0,1)$
所以l1、l2的方程分别为$y={k_1}(x+\sqrt{2})$、y=k2x+1
依题意联立:$\left\{{\begin{array}{l}{y={k_1}(x+\sqrt{2})}\\{\frac{x^2}{2}+{y^2}=λ}\end{array}}$⇒(1+2k12)x2+4$\sqrt{2}$k12x+4k12-2λ=0
又直线l1与椭圆G相切则△1=0(又0<λ<1),
即|k1|=$\frac{1}{{\sqrt{2}}}\sqrt{\frac{λ}{1-λ}}$…6分
依题意再联立:$\left\{{\begin{array}{l}{y={k_2}x+1}\\{\frac{x^2}{2}+{y^2}=λ}\end{array}}$⇒(1+2k22)x2+4k2x+2-2λ=0
又直线l2与椭圆G相切则△2=0(又0<λ<1),
即|k2|=$\frac{1}{{\sqrt{2}}}\sqrt{\frac{1-λ}{λ}}$…8分
故|k1k2|=$\frac{1}{2}$.…10分
(3)解:显然椭圆E:$\frac{x^2}{2}+{y^2}$=1,椭圆H:$\frac{x^2}{2}+\frac{y^2}{4}$=1.…11分
由椭圆H上的任意一点C(x0,y1)
于是$\frac{{{x_0}^2}}{2}+\frac{{{y_1}^2}}{4}$=1…12分
椭圆E上的点M(x0,y2),即$\frac{{{x_0}^2}}{2}+{y_2}$2=1又y1y2>0,则y1=2y2…13分
又$A(-\sqrt{2},0),B(\sqrt{2},0)$,则kAM=$\frac{y_2}{{{x_0}+\sqrt{2}}}$,kBC=$\frac{y_1}{{{x_0}-\sqrt{2}}}$…15分
又$\frac{y_2}{{{x_0}+\sqrt{2}}}•\frac{y_1}{{{x_0}-\sqrt{2}}}=\frac{y_2}{{{x_0}+\sqrt{2}}}•\frac{{2{y_2}}}{{{x_0}-\sqrt{2}}}=\frac{{2{y_2}^2}}{{{x_0}^2-2}}$=-1
所以AM⊥BC…16分.
点评 本题考查直线与椭圆的位置关系的综合应用,韦达定理以及直线的斜率的关系,考查分析问题解决问题的能力,转化思想以及分类讨论思想的应用.


 同步轻松练习系列答案
同步轻松练习系列答案科目:高中数学 来源: 题型:选择题
| A. | π | B. | 2 π | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
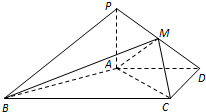 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
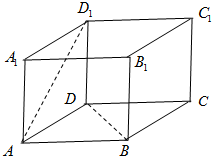 如图,已知直四棱柱ABCD-A1B1C1D1,DD1⊥底面ABCD,底面ABCD为平行四边形,∠DAB=45°,且AD,AB,AA1三条棱的长组成公比为$\sqrt{2}$的等比数列,
如图,已知直四棱柱ABCD-A1B1C1D1,DD1⊥底面ABCD,底面ABCD为平行四边形,∠DAB=45°,且AD,AB,AA1三条棱的长组成公比为$\sqrt{2}$的等比数列,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
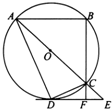 如图,AC是⊙O的直径,ABCD是圆内接四边形,DE与⊙O相切于点D,AC的延长线交DE于点E,BC的延长线交DE于点F,且AB∥DE.
如图,AC是⊙O的直径,ABCD是圆内接四边形,DE与⊙O相切于点D,AC的延长线交DE于点E,BC的延长线交DE于点F,且AB∥DE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
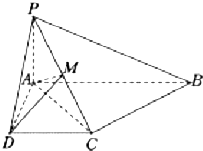 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,CB=$\sqrt{2}$,AB=2,PA=1.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,CB=$\sqrt{2}$,AB=2,PA=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com