
分析 (1)根据逆否命题的结论,写出原命题的条件,再写出M后解题.
(2)根据逆命题,否命题,逆否命题的定义进行求解即可.
解答 解:(1)设命题M表述为:若p,则q,那么由题意知其中的结论q为:x1或x2是方程x2+2x-3=0的两个根.
而条件p的否定形式 p为:x1+x2≠-2,或x1x2≠-3,故 p的否定形式即p为:x1+x2=-2且x1x2=-3.
所以命题M为:若x1+x2=-2且x1x2=-3,则x1或x2是方程x2+2x-3=0的两个根.
(2)M的逆命题为:若x1或x2是方程x2+2x-3=0的两个根,则x1+x2=-2且x1x2=-3.
逆否命题为:若x1或x2不是方程x2+2x-3=0的两个根,则x1+x2≠-2,或x1x2≠-3.
否命题为:若x1+x2≠-2,或x1x2≠-3,则x1或x2不是方程x2+2x-3=0的两个根.
点评 本题主要考查四种命题的求解,根据条件求出命题M是解决本题的关键.


科目:高中数学 来源: 题型:解答题
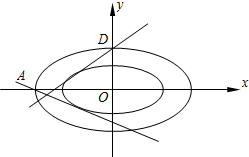 设椭圆E1的长半轴长为a1、短半轴长为b1,椭圆E2的长半轴长为a2、短半轴长为b2,若$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$,则我们称椭圆E1与椭圆E2是相似椭圆.已知椭圆E:$\frac{x^2}{2}$+y2=1,其左顶点为A、右顶点为B.
设椭圆E1的长半轴长为a1、短半轴长为b1,椭圆E2的长半轴长为a2、短半轴长为b2,若$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$,则我们称椭圆E1与椭圆E2是相似椭圆.已知椭圆E:$\frac{x^2}{2}$+y2=1,其左顶点为A、右顶点为B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
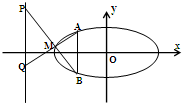 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,直线l:x-y+1=0经过C的上顶点.又,直线x=-1与C相较于A、B两点,M是C上异于A、B的任意一点,直线AM、BM分别交直线x=-4于两点P、Q.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,直线l:x-y+1=0经过C的上顶点.又,直线x=-1与C相较于A、B两点,M是C上异于A、B的任意一点,直线AM、BM分别交直线x=-4于两点P、Q.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃兰州一中高三9月月考数学(文)试卷(解析版) 题型:选择题
设集合A={x|x>a},集合B={-1,1,2},若A∩B=B,则实数a的取值范围是( )
A.(1,+∞) B.(-∞,1) C.(-1,+∞) D.(-∞,-1)
查看答案和解析>>
科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:解答题
已知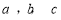 分别是
分别是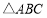 的内角
的内角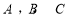 所对的边长,且
所对的边长,且 ,满
,满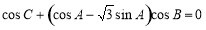 .
.
(1)求角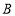 的大小;
的大小;
(2)若点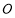 是
是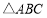 外一点,
外一点,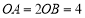 ,记
,记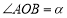 ,用含
,用含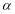 的三角函数式表示平面四边形
的三角函数式表示平面四边形 面积并求面积的最大值.
面积并求面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com