
分析 因为$\overrightarrow{a}$,$\overrightarrow{b}$均为单位向量,它们夹角为60,所以可求出它们的模以及数量积,欲求|$\overrightarrow{a}$+2$\overrightarrow{b}$|,只需自身平方再开方即可,这样就可出现两向量的模与数量积,把前面所求代入即可.
解答 解:∵$\overrightarrow{a}$,$\overrightarrow{b}$均为单位向量,它们夹角为60°,
∴|$\overrightarrow{a}$+2$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+4|$\overrightarrow{b}$|2+4$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|2+4|$\overrightarrow{b}$|2+4|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos60°=1+4+4×1×1×$\frac{1}{2}$=7,
∴|$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{7}$,
故答案为:$\sqrt{7}$
点评 本题考查了单位向量,数量积的概念,以及向量的模的求法,属于向量的综合运算.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
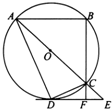 如图,AC是⊙O的直径,ABCD是圆内接四边形,DE与⊙O相切于点D,AC的延长线交DE于点E,BC的延长线交DE于点F,且AB∥DE.
如图,AC是⊙O的直径,ABCD是圆内接四边形,DE与⊙O相切于点D,AC的延长线交DE于点E,BC的延长线交DE于点F,且AB∥DE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃兰州一中高三9月月考数学(文)试卷(解析版) 题型:选择题
已知某地区中小学生人数和近视情况分别如图1和如图2所示,为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取 的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )


A.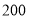 ,
,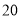 B.
B. ,
,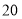 C.
C.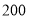 ,
, D.
D. ,
,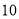
查看答案和解析>>
科目:高中数学 来源:2017届甘肃兰州一中高三9月月考数学(理)试卷(解析版) 题型:选择题
已知某地区中小学生人数和近视情况分别如图1和如图2所示,为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取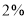 的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )


A.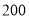 ,
,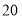 B.
B.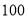 ,
, C.
C. ,
,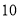 D.
D.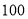 ,
,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com