
分析 过D作DG∥AC,可证明△AEF≌△CEG,可得AF=DG,由三角形中位线定理可得DG=$\frac{1}{2}$CF,可证得结论.
解答  证明:如图,过D作DG∥AC,则∠EAF=∠EDG,
证明:如图,过D作DG∥AC,则∠EAF=∠EDG,
∵AD是△ABC的中线,
∴D为BC中点,
∴G为BF中点,
∴DG=$\frac{1}{2}$CF,
∵E为AD中点,
∴AE=DE,
在△AEF和△DEG中,$\left\{\begin{array}{l}{∠EAF=∠EDG}\\{AE=DE}\\{∠AEF=∠DEG}\end{array}\right.$,
∴△AEF≌△DEG(ASA),
∴DG=AF,
∴AF=$\frac{1}{2}$CF,
∴AC:AF=3.
故答案为:3.
点评 本题主要考查三角形中位线定理,作辅助线构造三角形中位线找到GD和AF、CF的关系是解题的关键.


科目:高中数学 来源: 题型:解答题
| 青年人 | 中年人 | 合计 | |
| 经常使用微信 | |||
| 不经常使用微信 | |||
| 合计 |
| P(k2≥k) | 0.010 | 0.001 |
| k | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高一 | 高二 | 总计 | |
| 合格人数 | 70 | x | 150 |
| 不合格人数 | y | 20 | 50 |
| 总计 | 100 | 100 | 200 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(k2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
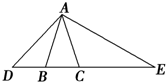 如图,在等腰三角形ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB•CE.
如图,在等腰三角形ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB•CE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(理)试卷(解析版) 题型:解答题
选修4—1:几何证明选讲
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点.
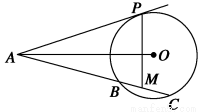
(1)证明:A、P、O、M四点共圆;
(2)求∠OAM+∠APM的大小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com