
分析 (1)依题意:设P曲线Γ上的任意一点,利用椭圆的定义,判断P的轨迹是以F1,F2为焦点,长轴长2a=4的椭圆.求出a,b,即可得到椭圆的方程.
(2)设出直线方程,联立直线与椭圆方程,利用韦达定理以及判别式,结合以AB为直径的圆恰好过椭圆的右焦点,求解m的值,即可求解直线方程.
解答 解:(1)依题意:设P曲线Γ上的任意一点,则|PF1|+|PF2|=4>|F1F2|=2,
所以P的轨迹是以F1,F2为焦点,长轴长2a=4的椭圆.
$a=2,c=1,b=\sqrt{3}$,则曲线方程:$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(4分)
(2)过Q(4,0)的直线l设为:x=my+4,
联立$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{3}=1\\ x=my+4\end{array}\right.$,得∴(3m2+4)y2+24my+36=0,
所以$\left\{\begin{array}{l}△>0\\{y_1}+{y_2}=\frac{-24m}{{3{m^2}+4}}\\{y_1}{y_2}=\frac{36}{{3{m^2}+4}}\end{array}\right.$…(6分),
以AB为直径的圆恰好过椭圆的右焦点,F(1,0).
A,B坐标分别为(x1,y1),(x2,y2),
∴$\overrightarrow{FA}•\overrightarrow{FB}=0$…(7分)
即$({x_1}-1)({x_2}-1)+{y_1}{y_2}\;=({m^2}+1){y_1}{y_2}+3m({y_1}+{y_2})+9=0$…(8分)
∴$\frac{{36({m^2}+1)}}{{3{m^2}+4}}+\frac{{-72{m^2}}}{{3{m^2}+4}}+9=0$…(9分) 解得:$m=±2\sqrt{2}$…(10分)
此时△=(24m)2-4×36(3m2+4)=144m2-576=576>0…(11分)
所以所求的直线方程为:$x±2\sqrt{2}y-4=0$…(12分)
点评 本题考查轨迹方程的求法,椭圆的定义的应用,直线与椭圆的位置关系的综合应用,考查转化思想以及设而不去方法的应用,考查分析问题解决问题的能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 网友 | 强烈关注 | 一般关注 | 合计 |
| 重庆市 | a= | b= | |
| 四川省 | c= | d= | |
| 合计 |
| P(K2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃兰州一中高三9月月考数学(文)试卷(解析版) 题型:选择题
已知某地区中小学生人数和近视情况分别如图1和如图2所示,为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取 的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )


A.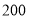 ,
,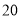 B.
B. ,
,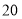 C.
C.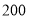 ,
, D.
D. ,
,
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(理)试卷(解析版) 题型:解答题
已知c>0,设命题p:函数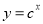 为减函数.命题q:当
为减函数.命题q:当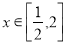 时,函数f(x)=x+
时,函数f(x)=x+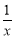 >
>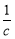 恒成立.如果“p∨q”为真命题,“p∧q”为假命题,求c的取值范围.
恒成立.如果“p∨q”为真命题,“p∧q”为假命题,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com