
分析 (Ⅰ)4个外地旅游小组共有54=625种不同的选法;
(Ⅱ)由4个旅游小组选择的线路互不相同的选法,共有$A_5^4=120$种选法;
(Ⅲ)求得所以的基本事件,采用分类法求得有且只有两条线路被选中的基本事件,根据概率公式即可求得P=$\frac{m}{n}$.
解答 解:(Ⅰ)这是一个“可重复的排列”问题,由每个旅游小组共有5中选法,
4个外地旅游小组共有54=625种不同的选法;
(Ⅱ)4个旅游小组选择的线路互不相同的选法共有$A_5^4=120$种选法;
(Ⅲ)所有基本事件数是n=54=625,依题意,4个小组去走2条线路,则4个旅游小组须分为“两堆”,一种分法是1
对3(不均分),一种分法是2对2(均分),
于是,满足题意的基本事件数是m=$C_5^2(C_4^1C_3^3A_2^2+\frac{C_4^2C_2^2}{A_2^2}•A_2^2)=140$,
∴所求概率为P=$\frac{140}{625}=\frac{28}{125}$.
点评 本题主要考查了分类计数原理原理的应用,古典概率的计算公式的应用,排列与组合的综合运用,对立事件的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
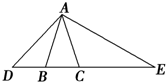 如图,在等腰三角形ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB•CE.
如图,在等腰三角形ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB•CE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:解答题
选修4—1:几何证明选讲
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点.
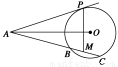
(1) 证明:A、P、O、M四点共圆;
(2)求∠OAM+∠APM的大小
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(理)试卷(解析版) 题型:选择题
已知函数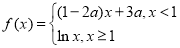 的值域为
的值域为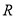 ,那么
,那么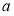 的取值范围是( )
的取值范围是( )
A. 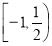 B.
B.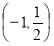 C.(-∞,-1] D.
C.(-∞,-1] D.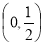
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com