
分析 (1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;(2)得到a≥$\frac{lnx}{{x}^{2}}$,记g(x)=$\frac{lnx}{{x}^{2}}$,求出函数的导数,得到g(x)的最大值,从而求出a的范围.
解答 解:(1)f′(x)=$\frac{1}{x}$-2ax=$\frac{1-2{ax}^{2}}{x}$,(x>0),
(i)若a≤0,则f′(x)>0,f(x)在(0,+∞)递增,
(ii)若a>0,由f′(x)=0,得:x=±$\frac{1}{\sqrt{2a}}$,
0<x<$\frac{1}{\sqrt{2a}}$时,f′(x)>0,f(x)在(0,$\frac{1}{\sqrt{2a}}$)递增,
x>$\frac{1}{\sqrt{2a}}$时,f′(x)<0,f(x)在($\frac{1}{\sqrt{2a}}$,+∞)递减;
(2)由f(x)≤0,得lnx-ax2≤0,a≥$\frac{lnx}{{x}^{2}}$,
记g(x)=$\frac{lnx}{{x}^{2}}$,则g′(x)=$\frac{1-2lnx}{{x}^{3}}$,x>0,
当x>$\sqrt{e}$时,g′(x)<0,g(x)在($\sqrt{e}$,+∞)递减,
0<x<$\sqrt{e}$时,g′(x)>0,g(x)在(0,$\sqrt{e}$)递增,
∴g(x)max=g($\sqrt{e}$)=$\frac{1}{2e}$,
a≥$\frac{1}{2e}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道中档题.


科目:高中数学 来源: 题型:填空题
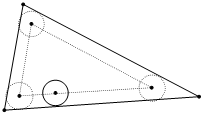 已知一个三角形的周长和面积分别是84、210,一个单位圆在它的内部沿着三边匀速无摩擦地滚动一周后回到原来的位置(如图),则这个三角形的内部以及边界没有被单位圆滚过的部分的面积是84-π.
已知一个三角形的周长和面积分别是84、210,一个单位圆在它的内部沿着三边匀速无摩擦地滚动一周后回到原来的位置(如图),则这个三角形的内部以及边界没有被单位圆滚过的部分的面积是84-π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
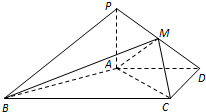 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,弦AB与CD相交于圆O内一点E,过E作BC的平行线与AD的延长线交于点P,且PD=2DA.
如图,弦AB与CD相交于圆O内一点E,过E作BC的平行线与AD的延长线交于点P,且PD=2DA.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
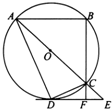 如图,AC是⊙O的直径,ABCD是圆内接四边形,DE与⊙O相切于点D,AC的延长线交DE于点E,BC的延长线交DE于点F,且AB∥DE.
如图,AC是⊙O的直径,ABCD是圆内接四边形,DE与⊙O相切于点D,AC的延长线交DE于点E,BC的延长线交DE于点F,且AB∥DE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 网友 | 强烈关注 | 一般关注 | 合计 |
| 重庆市 | a= | b= | |
| 四川省 | c= | d= | |
| 合计 |
| P(K2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com