
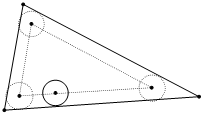
 已知一个三角形的周长和面积分别是84、210,一个单位圆在它的内部沿着三边匀速无摩擦地滚动一周后回到原来的位置(如图),则这个三角形的内部以及边界没有被单位圆滚过的部分的面积是84-π.
已知一个三角形的周长和面积分别是84、210,一个单位圆在它的内部沿着三边匀速无摩擦地滚动一周后回到原来的位置(如图),则这个三角形的内部以及边界没有被单位圆滚过的部分的面积是84-π. 分析 由图知,要求的面积有两部分:
①三角形的内部被圆滚过的部分是个三角形,且与原三角形相似,已知了原三角形的周长和面积,可求得原三角形的内切圆半径,进而可得三角形内部被圆滚过部分的三角形的内切圆半径,即可得到两个三角形的相似比,根据相似三角形的性质可求得此三角形的周长和面积;
②三角形边界的三个角的面积;连接单位圆的圆心和原三角形的三顶点,先求得构成的6个小直角三角形的面积,而3个扇形正好构成一个圆,由此可得原三角形边界三个角的面积;
综合①②的面积,即可得所求的值.
解答 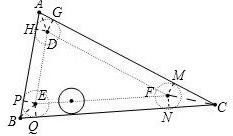 解:如图.
解:如图.
设△ABC的内切圆半径为R,△DEF的内切圆半径为r;
依题意有:$\frac{1}{2}$×84×R=210,即R=5;
易知:△DEF∽△ABC,且r:R=4:5,
∴C△DEF=$\frac{4}{5}$C△ABC=67.2;
易知:被圆滚过的三角形内部的三角形也和△ABC相似;
且其内切圆半径为:R-2=3,即其面积=$(\frac{3}{5})^{2}$S△ABC=75.6;
由图知:S四边形AHDG=2S△AGD=AG•1=AG,同理S四边形PEQB=BQ,S四边形CNFM=CM;
∴S四边形AHDG+S四边形PEQB+S四边形CNFM=AG+CM+BQ=$\frac{1}{2}$(C△ABC-C△DEF)=8.4;
而S扇形DHG+S扇形PEQ+S扇形FMN=S单位圆=π,
∴所求的面积=75.6+8.4-π=84-π.
故答案为:84-π.
点评 此题主要考查的是图形面积的求法,涉及到切线的性质、扇形面积的计算方法、相似三角形以及三角形内切圆半径的求法等知识;需要注意的有两点:
①被圆滚过的三角形内部的三角形与原三角形相似,②原三角形边界的三个扇形正好构成一个单位圆.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:选择题
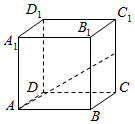 在棱长为1的正方体ABCD-A1B1C1D1中,点F是棱CC1的中点,P是正方体表面上的一点,若D1P⊥AF,则线段D1P长度的取值范围是( )
在棱长为1的正方体ABCD-A1B1C1D1中,点F是棱CC1的中点,P是正方体表面上的一点,若D1P⊥AF,则线段D1P长度的取值范围是( )| A. | (0,$\sqrt{2}$) | B. | (0,$\frac{\sqrt{34}}{4}$] | C. | (0,$\frac{3}{2}$] | D. | (0,$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在平角坐标系xOy中,椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{1}{2}$,且过点$(0,\sqrt{3})$,椭圆C的长轴的两端点为A,B,点P为椭圆上异于A,B的动点,定直线x=4与直线PA、PB分别交于M,N两点.
在平角坐标系xOy中,椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{1}{2}$,且过点$(0,\sqrt{3})$,椭圆C的长轴的两端点为A,B,点P为椭圆上异于A,B的动点,定直线x=4与直线PA、PB分别交于M,N两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 青年人 | 中年人 | 合计 | |
| 经常使用微信 | |||
| 不经常使用微信 | |||
| 合计 |
| P(k2≥k) | 0.010 | 0.001 |
| k | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
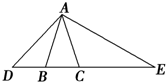 如图,在等腰三角形ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB•CE.
如图,在等腰三角形ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB•CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com