
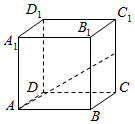
 在棱长为1的正方体ABCD-A1B1C1D1中,点F是棱CC1的中点,P是正方体表面上的一点,若D1P⊥AF,则线段D1P长度的取值范围是( )
在棱长为1的正方体ABCD-A1B1C1D1中,点F是棱CC1的中点,P是正方体表面上的一点,若D1P⊥AF,则线段D1P长度的取值范围是( )| A. | (0,$\sqrt{2}$) | B. | (0,$\frac{\sqrt{34}}{4}$] | C. | (0,$\frac{3}{2}$] | D. | (0,$\sqrt{3}$] |
分析 由P是正方体表面上的一点,且D1P⊥AF,通过建立空间直角坐标系,数量积运算性质及其正方体的性质即可得出.
解答 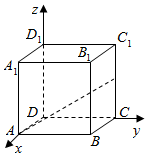 解:由P是正方体表面上的一点,且D1P⊥AF.建立如图所示的空间直角坐标系.
解:由P是正方体表面上的一点,且D1P⊥AF.建立如图所示的空间直角坐标系.
①由D1B1⊥对角面ACC1A1,则取B1点时,满足D1B1⊥AF,此时线段D1P长度=$\sqrt{2}$.
②设点Q在直线AB上,则Q(1,t,0),$\overrightarrow{{D}_{1}Q}$=(1,t,-1),$\overrightarrow{AF}$=$(-1,1,\frac{1}{2})$,
则$\overrightarrow{{D}_{1}Q}$•$\overrightarrow{AF}$=-1+t-$\frac{1}{2}$=0,解得t=$\frac{3}{2}$.此时$|\overrightarrow{{D}_{1}P}|$=$\frac{2}{3}$|$\overrightarrow{{D}_{1}Q}$|=$\frac{2}{3}\sqrt{(\sqrt{2})^{2}+(\frac{3}{2})^{2}}$=$\frac{\sqrt{17}}{3}$$<\sqrt{2}$.
由对称性可得:线段D1P长度取得最大值D1B=$\sqrt{2}$,
∴线段D1P长度的取值范围是(0,$\sqrt{2}$].
故选:A.
点评 本题考查了正方体的性质、线线线面垂直的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 性别 | 晕机 | 不晕机 | 合计 |
| 男 | 24 | 31 | 55 |
| 女 | 8 | 26 | 34 |
| 合计 | 32 | 57 | 89 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{13i}{5}$ | B. | -$\frac{13}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{13}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
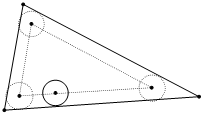 已知一个三角形的周长和面积分别是84、210,一个单位圆在它的内部沿着三边匀速无摩擦地滚动一周后回到原来的位置(如图),则这个三角形的内部以及边界没有被单位圆滚过的部分的面积是84-π.
已知一个三角形的周长和面积分别是84、210,一个单位圆在它的内部沿着三边匀速无摩擦地滚动一周后回到原来的位置(如图),则这个三角形的内部以及边界没有被单位圆滚过的部分的面积是84-π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com