练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．已知集合A={x|2x2-3x-5＜0}，B={x|y=log2（1-x）}，则A∩（∁RB）=[1，$\frac{5}{2}$）．

    分析 求出A中不等式的解集确定出A，求出B中x的范围确定出B，找出A与B补集的交集即可．

    解答 解：由A中不等式变形得：（2x-5）（x+1）＜0，
    解得：-1＜x＜$\frac{5}{2}$，即A=（-1，$\frac{5}{2}$），
    由B中y=log2（1-x），得到1-x＞0，即x＜1，
    ∴B=（-∞，1），即∁RB=[1，+∞），
    则A∩（∁RB）=[1，$\frac{5}{2}$），
    故答案为：[1，$\frac{5}{2}$）

    点评 此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    18．已知ab=1（a，b＞0），则$\frac{1}{a+1}$+$\frac{9}{b+9}$的最大值是$\frac{3}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．某超市五一促销，随机对10～60岁的人群抽查了n人，调查的每个人若能完整写出5个或5个以上外国节日，则能获得20元优惠券的奖励，若能完整写出8个或8个以上中国传统节日就能获得30元优惠券，调查的每个人都同时回答了这两个问题，统计结果如下表
    （Ⅰ）若以表中的频率近似看作各年龄段回答问题获得优惠劵的概率，组织者随机请一个家庭中的两名成员（大人42岁，孩子16岁）回答这两个问题，两个调查相互独立均无影响，分别写出这个家庭两个成员获得奖励的分布列并求该家庭获得奖励的期望；
    （Ⅱ）求该家庭获得奖励为50元优惠券的概率．
    年龄段外国传统节日中国传统节日
    获优惠劵的人数占本组人数频率获优惠券的人数占本组人数频率
    [10，20）30a300.5
    [20，30）480.8360.6
    [30，40）360.6480.8
    [40，50）200.524b
    [50，60]40.2160.8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

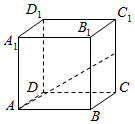    16．在棱长为1的正方体ABCD-A1B1C1D1中，点F是棱CC1的中点，P是正方体表面上的一点，若D1P⊥AF，则线段D1P长度的取值范围是（　　）
    A．（0，$\sqrt{2}$）B．（0，$\frac{\sqrt{34}}{4}$]C．（0，$\frac{3}{2}$]D．（0，$\sqrt{3}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知cosα=$\frac{\sqrt{2}}{3}$，α∈（$\frac{3π}{2}$，2π），则sin（$α+\frac{5π}{6}$）的值为（　　）
    A．$\frac{\sqrt{21}+\sqrt{2}}{6}$B．$\frac{\sqrt{21}-\sqrt{2}}{6}$C．$\frac{-\sqrt{21}+\sqrt{2}}{6}$D．$\frac{-\sqrt{21}-\sqrt{2}}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

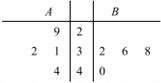    13．将某商场A，B两个品牌店在某日14：00-18：00四个时段（每个小时作为一个时段）的客流量统计并绘制成如图所示的茎叶图．
    （1）若从B商场中任选2个时段的数据，求这2个时段的数据均多于A商场数据平均数的概率；
    （2）从这8个数据中随机选取3个，设这3个数据中大于35的个数为X，求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知m，n，l是三条不同直线，α，β，γ是三个不同平面，则下列说法正确的是（　　）
    A．若l∥n，n∥β，则l∥βB．若α⊥β，n∥α，m∥β，则m⊥n
    C．若α⊥β，β⊥γ，则α∥γD．若l⊥α，l⊥β，则α∥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．定积分$\int_{-1}^1$exdx的值为$e-\frac{1}{e}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．某公司200名员工中$\frac{90}{100}$的人使用微信，其中每天使用微信时间在一小时内有关60人，其余员工每天使用微信时间在一小时以上．若将员工分成青年（年龄小于40岁）和中年（年龄不小于40岁）二个阶段，那么使用微信的人中$\frac{75}{100}$是青年人．若规定：每天使用微信时间在一小时以上为经常使用微信，那么经常使用微信员工中$\frac{2}{3}$是青年人．
    （1）若要调查该公司使用微信的员工经常使用微信与年龄关系，列出2×2列联表
    青年人中年人合计
    经常使用微信
    不经常使用微信
    合计
    （1）由列联表中所得数据判断是否有$\frac{99.9}{100}$把握认为“经常使用微信年龄有关”．
    （2）采用分层抽样方法从“经常使用微信“的人中抽取6人，从这6人中任选2人，求选出2人均是青年人的概率．
    P（k2≥k）0.0100.001
    k6.63510.828
    ${k^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．

    查看答案和解析>>

    同步练习册答案