
| A. | $\frac{\sqrt{21}+\sqrt{2}}{6}$ | B. | $\frac{\sqrt{21}-\sqrt{2}}{6}$ | C. | $\frac{-\sqrt{21}+\sqrt{2}}{6}$ | D. | $\frac{-\sqrt{21}-\sqrt{2}}{6}$ |
分析 cosα=$\frac{\sqrt{2}}{3}$,α∈($\frac{3π}{2}$,2π),由同角三角函数的基本关系,即可求得sinα的值,根据两角和正弦公式将sin($α+\frac{5π}{6}$)展开即可求得sin($α+\frac{5π}{6}$)的值.
解答 解:因为cosα=$\frac{\sqrt{2}}{3}$,α∈($\frac{3π}{2}$,2π),
∴sinα=-$\frac{\sqrt{7}}{3}$,
sin($α+\frac{5π}{6}$)=sinαcos$\frac{5π}{6}$+cosαsin$\frac{5π}{6}$=-$\frac{\sqrt{7}}{3}$×(-$\frac{\sqrt{3}}{2}$)+$\frac{\sqrt{2}}{3}$×$\frac{1}{2}$=$\frac{\sqrt{21}+\sqrt{2}}{6}$,
故答案选:A.
点评 本题考查三角恒等变换,三角函数诱导公式,考查学生的基本运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
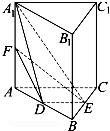 在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=1,AA1=2,D、E分别为棱AB、BC的中点,点F在棱AA1上.
在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=1,AA1=2,D、E分别为棱AB、BC的中点,点F在棱AA1上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=ex+e-x | B. | f(x)=ex-e-x | C. | f(x)=x|x| | D. | f(x)=cos(x-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | 2 π | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com