
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x+2y-4≤0}\\{x-y+a≤0}\\{x≥1}\end{array}\right.$,作出可行域如图,
z=$\frac{3}{2}$x+y,可得y=-$\frac{3}{2}x+z$,平移直线y=-$\frac{3}{2}x+z$,由图象可知,当直线经过点A时,
z的最大值为4,
由$\left\{\begin{array}{l}{\frac{3}{2}x+y=4}\\{x+2y-4=0}\end{array}\right.$,可得A(2,1),直线的截距最大,此时z也最大,
可得:2-1+a=0.解得a=-1.
故答案为:-1.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄段 | 外国传统节日 | 中国传统节日 | ||
| 获优惠劵的人数 | 占本组人数频率 | 获优惠券的人数 | 占本组人数频率 | |
| [10,20) | 30 | a | 30 | 0.5 |
| [20,30) | 48 | 0.8 | 36 | 0.6 |
| [30,40) | 36 | 0.6 | 48 | 0.8 |
| [40,50) | 20 | 0.5 | 24 | b |
| [50,60] | 4 | 0.2 | 16 | 0.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sin$\frac{π}{6}$)>f(cos$\frac{π}{6}$) | B. | f(sin$\frac{π}{3}$)>f(cos$\frac{π}{3}$) | C. | f(sin$\frac{2π}{3}$)>f(cos$\frac{2π}{3}$) | D. | f(sin$\frac{3π}{4}$)>f(cos$\frac{3π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
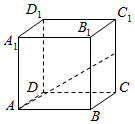 在棱长为1的正方体ABCD-A1B1C1D1中,点F是棱CC1的中点,P是正方体表面上的一点,若D1P⊥AF,则线段D1P长度的取值范围是( )
在棱长为1的正方体ABCD-A1B1C1D1中,点F是棱CC1的中点,P是正方体表面上的一点,若D1P⊥AF,则线段D1P长度的取值范围是( )| A. | (0,$\sqrt{2}$) | B. | (0,$\frac{\sqrt{34}}{4}$] | C. | (0,$\frac{3}{2}$] | D. | (0,$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{21}+\sqrt{2}}{6}$ | B. | $\frac{\sqrt{21}-\sqrt{2}}{6}$ | C. | $\frac{-\sqrt{21}+\sqrt{2}}{6}$ | D. | $\frac{-\sqrt{21}-\sqrt{2}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l∥n,n∥β,则l∥β | B. | 若α⊥β,n∥α,m∥β,则m⊥n | ||
| C. | 若α⊥β,β⊥γ,则α∥γ | D. | 若l⊥α,l⊥β,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在平角坐标系xOy中,椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{1}{2}$,且过点$(0,\sqrt{3})$,椭圆C的长轴的两端点为A,B,点P为椭圆上异于A,B的动点,定直线x=4与直线PA、PB分别交于M,N两点.
在平角坐标系xOy中,椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{1}{2}$,且过点$(0,\sqrt{3})$,椭圆C的长轴的两端点为A,B,点P为椭圆上异于A,B的动点,定直线x=4与直线PA、PB分别交于M,N两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com