
分析 (1)根据导数的几何意义解出切点坐标和斜率,带入直线的点斜式方程;
(2)由题意可得(x-lnx)a≤x2-2x,记F(x)=x-lnx,求出导数,求得最小值1,运用参数分离可得a≤$\frac{{x}^{2}-2x}{x-lnx}$,求出导数,求得单调区间、极值和最值,即可得到a的范围;
(3)求出f(x)的导数,假设f(x)是“中值平均函数”,则存在A(x1,f(x1)),B(x2,f(x2))(0<x1<x2),求出切线的斜率,运用两点的斜率公式,可得$\frac{2a}{{x}_{1}+{x}_{2}}$,讨论a是否为0,构造函数求出导数,判断单调性,结合新定义,即可得到所求“中值平均切线”的条数.
解答 解:(1)解:(1)a=1时,f(x)=lnx+x2-4x,f′(x)=$\frac{1}{x}$+2x-4.
∴f(x)在x=1处的切线斜率k=f′(1)=-1,
∵f(1)=-3,
∴f(x)在x=1处的切线方程是y+3=-(x-1),即x+y+2=0,
∴函数在x=1处的切线方程为:x+y+2=0,
(2)由f(x)≥g(x),得(x-lnx)a≤x2-2x,
记F(x)=x-lnx(x>0),F′(x)=$\frac{x-1}{x}$,(x>0),
当0<x<1时,F′(x)<0,F(x)递减,
当x>1时,F′(x)>0,F(x)递增;
∴F(x)≥F(1)=1>0,
∴a≤$\frac{{x}^{2}-2x}{x-lnx}$,记G(x)=$\frac{{x}^{2}-2x}{x-lnx}$,x∈[$\frac{1}{e}$,e],
∴G′(x)=$\frac{(x-1)(x-2lnx+2)}{(x-lnx)^{2}}$,
∴x-2lnx+2=2(1-lnx)+x≥x>0,
∴x∈[$\frac{1}{e}$,e]时,G′(x)<0,G(x)递减;
x∈(1,e]时,G′(x)>0,G(x)递增;
∴G(x)min=G(1)=-1,∴a≤G(x)min=-1,
故实数a的取值范围为(-∞,-1];
(3)函数f(x)的定义域为(0,+∞),f′(x)=$\frac{a}{x}$+2x-4=$\frac{2{x}^{2}-4x+a}{x}$
若函数f(x)是“中值平均函数”,
则存在A(x1,f(x1)),B(x2,f(x2))(0<x1<x2)
使得f′(x0)=$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$,即$\frac{2a}{{x}_{1}+{x}_{2}}$+x1+x2-4=$\frac{a(ln{x}_{2}-ln{x}_{1})+{x}_{2}^{2}-{x}_{1}^{2}-4({x}_{2}-{x}_{1})}{{x}_{2}-{x}_{1}}$
∴$\frac{2a}{{x}_{1}+{x}_{2}}$=$\frac{a(ln{x}_{2}-{lnx}_{1})}{{x}_{2}-{x}_{1}}$(※)
①当a=0时,(※)对任意的0<x1<x2都成立,
∴函数f(x)是“中值平均函数”,且函数f(x)的“中值平均切线”有无数条;
②当a≠0时,有$\frac{2({x}_{2}-{x}_{1})}{{x}_{1}+{x}_{2}}$=ln$\frac{{x}_{2}}{{x}_{1}}$,
设t=$\frac{{x}_{2}}{{x}_{1}}$>1,则方程lnt=$\frac{2(t-1)}{t+1}$在区间(1,+∞)上有解,
记函数h(t)=lnt-$\frac{2(t-1)}{t+1}$,t>1,
则h′(t)=$\frac{1}{t}$-$\frac{4}{(t+1)^{2}}$=$\frac{(t-1)^{2}}{t(t+1)^{2}}$>0,
∴函数h(t)在区间(1,+∞)递增,
∵h(1)=0,
∴当t>1时,h(t)>h(1)=0,
即方程lnt-$\frac{2(t-1)}{t+1}$在区间(1,+∞)上无解,即函数f(x)不是“中值平均函数”;
综上,当a=0时,f(x)是“中值平均函数”,函数f(x)的“中值平均切线”有无数条;
当a≠0时,f(x)不是“中值平均函数”.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查不等式恒成立问题的解法,注意运用分离参数,考查新定义的理解和运用,注意运用分类讨论的思想方法,考查构造函数的方法,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
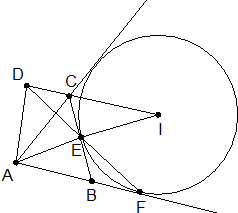 定义:和三角形一边和另两边的延长线同时相切的圆叫做三角形这边上的旁切圆.如图所示,已知:⊙I是△ABC的BC边上的旁切圆,E、F分别是切点,AD⊥IC于点D.
定义:和三角形一边和另两边的延长线同时相切的圆叫做三角形这边上的旁切圆.如图所示,已知:⊙I是△ABC的BC边上的旁切圆,E、F分别是切点,AD⊥IC于点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$] | B. | (-∞,-$\frac{\sqrt{2}}{2}$]∪[$\frac{\sqrt{2}}{2}$,+∞) | C. | [-$\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{2}}{2}$]∪[$\frac{\sqrt{2}}{2}$,$\frac{2\sqrt{5}}{5}$] | D. | (-$\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{2}}{2}$]∪[$\frac{\sqrt{2}}{2}$,$\frac{2\sqrt{5}}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 性别 | 晕机 | 不晕机 | 合计 |
| 男 | 24 | 31 | 55 |
| 女 | 8 | 26 | 34 |
| 合计 | 32 | 57 | 89 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
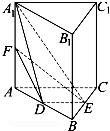 在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=1,AA1=2,D、E分别为棱AB、BC的中点,点F在棱AA1上.
在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=1,AA1=2,D、E分别为棱AB、BC的中点,点F在棱AA1上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com