
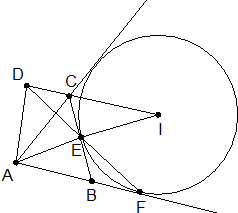
 定义:和三角形一边和另两边的延长线同时相切的圆叫做三角形这边上的旁切圆.如图所示,已知:⊙I是△ABC的BC边上的旁切圆,E、F分别是切点,AD⊥IC于点D.
定义:和三角形一边和另两边的延长线同时相切的圆叫做三角形这边上的旁切圆.如图所示,已知:⊙I是△ABC的BC边上的旁切圆,E、F分别是切点,AD⊥IC于点D.分析 (1)若设AC与⊙I的切点为M,那么又切线长定理知:∠MCI=∠ECI,即∠ACD=∠KCD,而CD⊥AK,可得两个条件:AC=CK,AD=DK;同样由切线长定理知:BE=BF,AF=AM=AC+CE,因此可得$\frac{KD}{DA}•\frac{AF}{FB}•\frac{BE}{EK}=1$,即可证得D、E、F三点共线.
(2)由于AB=AC,即△ABC是等腰三角形,而BC是⊙I的切线,即IE⊥BC,由切线长定理知AI平分∠CAB,即AI⊥BC,因此A、E、I三点共线,由此可得两组相似三角形:则△ABE∽△AIF,△ADI∽△CEI,根据第二组相似三角形得到的比例线段可求得⊙I的半径,根据第一组相似三角形可得AD、ID的比例关系,联立AI的长以及勾股定理可确定AD、DI的长;易知∠ADI、∠AFI都是直角,因此A、F、I、D四点共圆(以AI为直径),即可证得△DEI∽△AEF,根据DI、AF的长可得m、n的值,进而可根据韦达定理得出所求的一元二次方程.
解答 解:(1)结论:D、E、F三点是同在一条直线上.(1分)
证明:分别延长AD、BC交于点K,由旁切圆的定义及题中已知条件得:AD=DK,AC=CK,
再由切线长定理得:AC+CE=AF,BE=BF,(3分)
∴KE=AF.
∴$\frac{KD}{DA}•\frac{AF}{FB}•\frac{BE}{EK}=1$,由梅涅劳斯定理的逆定理可证D、E、F三点共线. (3分)
(2)∵AB=AC=5,BC=6,∴A、E、I三点共线,CE=BE=3,AE=4,
连结IF,则△ABE∽△AIF,△ADI∽△CEI,A、F、I、D四点共圆.(2分)
设⊙I的半径为r,则:$\frac{3}{r}=\frac{4}{8},r=6$,∴$AI=10,\frac{AD}{ID}=\frac{3}{6}$,即$AD=2\sqrt{5}$,$ID=4\sqrt{5}$,
∴由△AEF∽△DEI得:$m={(\frac{{4\sqrt{5}}}{8})^2}=\frac{5}{4},\frac{DE}{AE}=\frac{{4\sqrt{5}}}{8}=\frac{{\sqrt{5}}}{2},DE=2\sqrt{5}$,$\frac{IE}{EF}=\frac{{\sqrt{5}}}{2},EF=\frac{12}{5}\sqrt{5}$,
∴$n=\frac{5}{6}$. (4分)
∴$\left\{{\begin{array}{l}{\frac{m}{n}+\frac{n}{m}=\frac{13}{6}}\\{\frac{m}{n}•\frac{n}{m}=1}\end{array}}\right.$,
因此,由韦达定理可知:分别以$\frac{m}{n}、\frac{n}{m}$为两根且二次项系数为6的一个一元二次方程是6x2-13x+6=0. (3分)
点评 此题考查了切线的性质、切线长定理、三点共线的判定方法、相似三角形的判定和性质、梅氏定理、勾股定理以及韦达定理等知识的综合应用,难度较大.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(2,{e^{\frac{3}{2}}})$ | B. | $(\frac{3}{2},+∞)$ | C. | $(ln2,{e^{\frac{3}{2}}})$ | D. | $(ln2,\frac{3}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com