
| A. | 直角三角形 | B. | 等边三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
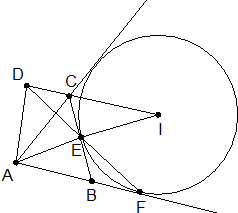 定义:和三角形一边和另两边的延长线同时相切的圆叫做三角形这边上的旁切圆.如图所示,已知:⊙I是△ABC的BC边上的旁切圆,E、F分别是切点,AD⊥IC于点D.
定义:和三角形一边和另两边的延长线同时相切的圆叫做三角形这边上的旁切圆.如图所示,已知:⊙I是△ABC的BC边上的旁切圆,E、F分别是切点,AD⊥IC于点D.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com