
分析 (1)曲线C:$\left\{\begin{array}{l}{x=\sqrt{3}cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数),利用平方关系可得普通方程.直线l的极坐标方程为ρcos(θ+$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$m(m>2),展开可得:$\frac{\sqrt{2}}{2}$ρ(cosθ-sinθ)=$\frac{\sqrt{2}}{2}$m,利用互化公式可得直角坐标方程.
(2)设与直线x-y-m=0平行且与椭圆相切的直线方程为x-y+t=0.把y=x+t代入椭圆方程可得:4x2+6tx+3t2-3=0,利用△=0,解得:t=±2.对t分类讨论,利用点到直线的距离公式即可得出m.
解答 解:(1)曲线C:$\left\{\begin{array}{l}{x=\sqrt{3}cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数),利用平方关系可得普通方程:$\frac{{x}^{2}}{3}$+y2=1.
直线l的极坐标方程为ρcos(θ+$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$m(m>2),展开可得:$\frac{\sqrt{2}}{2}$ρ(cosθ-sinθ)=$\frac{\sqrt{2}}{2}$m,化为直角坐标方程:x-y-m=0.
(2)设与直线x-y-m=0平行且与椭圆相切的直线方程为x-y+t=0.
把y=x+t代入椭圆方程可得:4x2+6tx+3t2-3=0,
令△=36t2-48(t2-1)=0,解得:t=±2.
当t=2时,方程为(2x+3)2=0,解得x=-$\frac{3}{2}$,代入椭圆方程可得:$\frac{3}{4}+{y}^{2}$=1,取y=$\frac{1}{2}$,可得切点P$(-\frac{3}{2},\frac{1}{2})$,则$\frac{|-\frac{3}{2}-\frac{1}{2}-m|}{\sqrt{2}}$=2,解得m=-2±2$\sqrt{2}$.经过验证都满足条件.
当t=-2时,方程为(2x-3)2=0,解得x=$\frac{3}{2}$,代入椭圆方程可得:$\frac{3}{4}+{y}^{2}$=1,取y=-$\frac{1}{2}$,可得切点P$(\frac{3}{2},-\frac{1}{2})$,则$\frac{|\frac{3}{2}+\frac{1}{2}-m|}{\sqrt{2}}$=2,解得m=2±2$\sqrt{2}$.经过验证都满足条件.
综上可得:取点P$(-\frac{3}{2},\frac{1}{2})$,m=-2±2$\sqrt{2}$.
取点P$(\frac{3}{2},-\frac{1}{2})$,m=2±2$\sqrt{2}$.
点评 本题考查了参数方程化为普通方程、直线与椭圆相切转化为一元二次方程的实数根与判别式的关系、点到直线的距离公式,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图三棱锥P-ABC中,PC⊥平面ABC,PC=$\frac{2}{\sqrt{3}}$,D是BC的中点,且△ADC是边长为2的正三角形,求二面角P-AB-C的大小.
如图三棱锥P-ABC中,PC⊥平面ABC,PC=$\frac{2}{\sqrt{3}}$,D是BC的中点,且△ADC是边长为2的正三角形,求二面角P-AB-C的大小.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
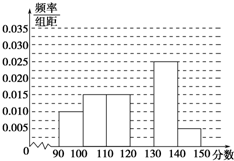 某校从参加高三模拟考试的学生中随机抽取100名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图,其中成绩在[130,150]的称为“优秀”,其它的称为“一般”,观察图形的信息,回答下列问题:
某校从参加高三模拟考试的学生中随机抽取100名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图,其中成绩在[130,150]的称为“优秀”,其它的称为“一般”,观察图形的信息,回答下列问题:| 数学成绩“优秀” | 数学成绩“一般” | 总计 | |
| 地理成绩“优秀” | 10 | 40 | 50 |
| 地理成绩“一般” | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | [1,3] | C. | [1,2] | D. | [0,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com