
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 求出双曲线的渐近线方程,结合直线平行的关系,建立斜率关系,利用离心率的定义进行转化求解即可.
解答 解:双曲线的焦点在x轴,则双曲线的渐近线方程为y=±$\frac{b}{a}$x,
直线$\sqrt{3}$x-y+4=0的斜截式方程为y=$\sqrt{3}$x+4,
∵双曲线渐近线与直线$\sqrt{3}$x-y+4=0平行,
则$\frac{b}{a}$=$\sqrt{3}$,即b=$\sqrt{3}$a,
平方得b2=3a2=c2-a2,
即c2=4a2,
则c=2a,
即离心率e=$\frac{c}{a}$=2.
故选:D.
点评 本题主要考查双曲线离心率的计算,结合双曲线渐近线的关系建立方程是解决本题的关键.


科目:高中数学 来源: 题型:选择题
 汉诺塔的游戏规则如下:如图有A,B,C三根套杆,在A上有n个大小不等的盘子,中间有孔可以套在杆子上面,大盘在下,小盘在下,现在要将A杆上面的所有盘子合部移动到C杆上面,每次只能移动一个盘子,且每根杆子上面的所有盘子大盘不能压在小盘上面;n个盘子全部移动完成后,所需的最少移动次数记为vn,例如v1=1,v2=3;请你耐心寻找规律,计算v5=( )
汉诺塔的游戏规则如下:如图有A,B,C三根套杆,在A上有n个大小不等的盘子,中间有孔可以套在杆子上面,大盘在下,小盘在下,现在要将A杆上面的所有盘子合部移动到C杆上面,每次只能移动一个盘子,且每根杆子上面的所有盘子大盘不能压在小盘上面;n个盘子全部移动完成后,所需的最少移动次数记为vn,例如v1=1,v2=3;请你耐心寻找规律,计算v5=( )| A. | 31 | B. | 15 | C. | 11 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
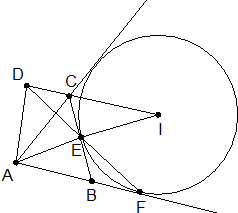 定义:和三角形一边和另两边的延长线同时相切的圆叫做三角形这边上的旁切圆.如图所示,已知:⊙I是△ABC的BC边上的旁切圆,E、F分别是切点,AD⊥IC于点D.
定义:和三角形一边和另两边的延长线同时相切的圆叫做三角形这边上的旁切圆.如图所示,已知:⊙I是△ABC的BC边上的旁切圆,E、F分别是切点,AD⊥IC于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
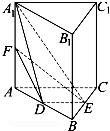 在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=1,AA1=2,D、E分别为棱AB、BC的中点,点F在棱AA1上.
在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=1,AA1=2,D、E分别为棱AB、BC的中点,点F在棱AA1上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com