
分析 (1)由f′(1)=2得a,从而可得f′(x)=lnx+2,在定义域内解不等式f′(x)>0,f′(x)<0可得函数的单调区间,从而求出函数的极值;
(2)不等式整理成k<$\frac{2f(x)-x}{x-1}$,令g(x)=$\frac{x+2xlnx}{x-1}$,只需求出g(x)的最小值即可.
解答 解:(1)f'(x)=a+lnx+1,
∵曲线y=f(x)在点(1,f(1))处的切线斜率为2,
∴f'(1)=a+1=2,∴a=1,
∴f'(x)=lnx+2,
当x∈(0,e-2)时,f'(x)<0,f(x)递减,
当x∈(e-2,+∞)时,f'(x)>0,f(x)递增,
∴f(x)的极小值是f(e-2)=-e-2,无极大值;
∴f(x)的单调递减区间为(0,e-2),单调递增区间为(e-2,+∞);
(2)2f(x)-(k+1)x+k>0,
∴k<$\frac{2f(x)-x}{x-1}$,∴k<$\frac{x+2xlnx}{x-1}$,
令g(x)=$\frac{x+2xlnx}{x-1}$,则g'(x)=$\frac{2x-3-2lnx}{{(x-1)}^{2}}$,
设h(x)=2x-3-2lnx,则h'(x)=2-$\frac{2}{x}$>0,
∴h(x)在(1,+∞)上为增函数,
∵h(2)=1-2ln2<0,h(3)=3-2ln3>0,
∴?x0∈(2,3),且h(x0)=0,
当x∈(1,x0)时,h(x)<0,g′(x)<0,g(x)在(1,x0)上单调递减;
当x∈(x0,+∞)时,h(x)>0,g′(x)>0,g(x)在(x0,+∞)上单调递增.
∴g(x)min=g(x0)=$\frac{{x}_{0}+{2x}_{0}l{nx}_{0}}{{x}_{0}-1}$,
∵h(x0)=2x0-3-2lnx0=0,
∴g(x0)=2x0,
∵x0∈(2,3),
∴k的最大值为4.
点评 本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与最值,解题时合理构造函数是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{21}+\sqrt{2}}{6}$ | B. | $\frac{\sqrt{21}-\sqrt{2}}{6}$ | C. | $\frac{-\sqrt{21}+\sqrt{2}}{6}$ | D. | $\frac{-\sqrt{21}-\sqrt{2}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在平角坐标系xOy中,椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{1}{2}$,且过点$(0,\sqrt{3})$,椭圆C的长轴的两端点为A,B,点P为椭圆上异于A,B的动点,定直线x=4与直线PA、PB分别交于M,N两点.
在平角坐标系xOy中,椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{1}{2}$,且过点$(0,\sqrt{3})$,椭圆C的长轴的两端点为A,B,点P为椭圆上异于A,B的动点,定直线x=4与直线PA、PB分别交于M,N两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 青年人 | 中年人 | 合计 | |
| 经常使用微信 | |||
| 不经常使用微信 | |||
| 合计 |
| P(k2≥k) | 0.010 | 0.001 |
| k | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
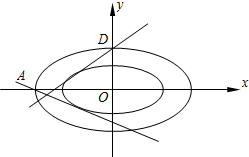 设椭圆E1的长半轴长为a1、短半轴长为b1,椭圆E2的长半轴长为a2、短半轴长为b2,若$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$,则我们称椭圆E1与椭圆E2是相似椭圆.已知椭圆E:$\frac{x^2}{2}$+y2=1,其左顶点为A、右顶点为B.
设椭圆E1的长半轴长为a1、短半轴长为b1,椭圆E2的长半轴长为a2、短半轴长为b2,若$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$,则我们称椭圆E1与椭圆E2是相似椭圆.已知椭圆E:$\frac{x^2}{2}$+y2=1,其左顶点为A、右顶点为B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com