
分析 (1)由题意可得0<m<1,由椭圆方程可得a,b,解m的方程可得m的值;
(2)△PF1F2不能成为直角三角形.求得椭圆的右顶点和焦点,以及△PF1F2的三边长,由勾股定理的逆定理,即可判断.
解答 解:(1)椭圆x2+my2=1的焦点在y轴上,
即有0<m<1,
由椭圆方程x2+$\frac{{y}^{2}}{\frac{1}{m}}$=1可得,
b=1,a=$\sqrt{\frac{1}{m}}$,
由长轴长是短轴长的2倍,可得$\sqrt{\frac{1}{m}}$=2,
解得m=$\frac{1}{4}$;
(2)△PF1F2不能成为直角三角形.
理由:椭圆方程x2+$\frac{{y}^{2}}{4}$=1,
可得a=2,b=1,c=$\sqrt{3}$,
即有短轴的右顶点为P(1,0),
焦点为F1(0,-$\sqrt{3}$),F2(0,$\sqrt{3}$),
|PF1|=|PF2|=2,|F1F2|=2$\sqrt{3}$,
由|PF1|2+|PF2|2≠|F1F2|2,
可得△PF1F2不为直角三角形.
点评 本题考查椭圆的方程和性质及运用,考查直角三角形的判断,化简整理的运算能力,属于基础题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
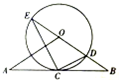 如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于点E、D,连接EC、CD.
如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于点E、D,连接EC、CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 满意 | 不满意 | 总计 | |
| 男性/人 | 42 | 8 | 50 |
| 女性/人 | 28 | 22 | 50 |
| 总计/人 | 70 | 30 | 100 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.843 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
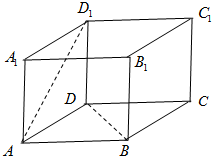 如图,已知直四棱柱ABCD-A1B1C1D1,DD1⊥底面ABCD,底面ABCD为平行四边形,∠DAB=45°,且AD,AB,AA1三条棱的长组成公比为$\sqrt{2}$的等比数列,
如图,已知直四棱柱ABCD-A1B1C1D1,DD1⊥底面ABCD,底面ABCD为平行四边形,∠DAB=45°,且AD,AB,AA1三条棱的长组成公比为$\sqrt{2}$的等比数列,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com