
| A. | 9×29 | B. | 10×29 | C. | 10×210 | D. | 10×211 |
分析 数列{an}中,a1=1,an+1=2an+2n,变形为$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{{a}_{n}}{{2}^{n}}$=$\frac{1}{2}$,利用等差数列的通项公式即可得出.
解答 解:∵数列{an}中,a1=1,an+1=2an+2n,
∴$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{{a}_{n}}{{2}^{n}}$=$\frac{1}{2}$,
∴数列{$\frac{{a}_{n}}{{2}^{n}}$}是等差数列,首项为$\frac{1}{2}$,公差为$\frac{1}{2}$.
∴$\frac{{a}_{n}}{{2}^{{n}^{\;}}}$=$\frac{1}{2}$+$\frac{1}{2}$(n-1)=$\frac{1}{2}$n,
∴an=n•2n-1.
则a10=10×29.
故选:B
点评 本题考查了递推关系、等差数列的通项公式,考查了推理能力与计算能力,属于中档题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
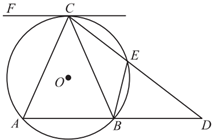 如图,已知CF是圆O的切线,C为切点,弦AB∥CF,E为圆周上一点,CE交AB的延长线于点D,弧$\widehat{AB}$=弧$\widehat{BC}$.求证:
如图,已知CF是圆O的切线,C为切点,弦AB∥CF,E为圆周上一点,CE交AB的延长线于点D,弧$\widehat{AB}$=弧$\widehat{BC}$.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
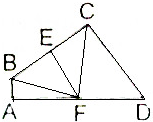 如图所示,四边形ABCD中,AB=1,AD=7,BC=CD=5,∠BAD=∠BCD=90°.
如图所示,四边形ABCD中,AB=1,AD=7,BC=CD=5,∠BAD=∠BCD=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
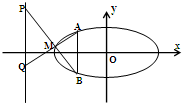 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,直线l:x-y+1=0经过C的上顶点.又,直线x=-1与C相较于A、B两点,M是C上异于A、B的任意一点,直线AM、BM分别交直线x=-4于两点P、Q.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,直线l:x-y+1=0经过C的上顶点.又,直线x=-1与C相较于A、B两点,M是C上异于A、B的任意一点,直线AM、BM分别交直线x=-4于两点P、Q.查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:选择题
设函数f(x)=logax(a>0,且a≠1),若f(x1x2…x2 017)=8,则f(x)+f(x)+…+f(x)的值等于( )
A.4 B.8 C.16 D.2loga8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com